Category: math

Finding the great divide

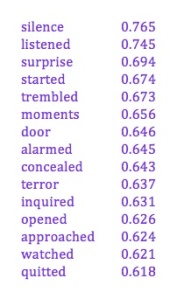
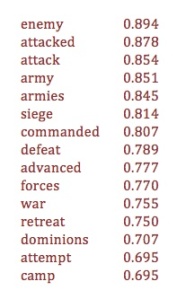
Last year, Jordan Sellers and I published an article in Modern Language Quarterly, trying to trace the “great divide” that is supposed to open up between mass culture and advanced literary taste around the beginning of the twentieth century.

I’m borrowing the phrase “great divide” from Andreas Huyssen, but he’s not the only person to describe the phenomenon. Whether we explain it neutrally as a consequence of widespread literacy, or more skeptically as the rise of a “culture industry,” literary historians widely agree that popularity and prestige parted company in the twentieth century. So we were surprised not to be able to measure the widening gap.

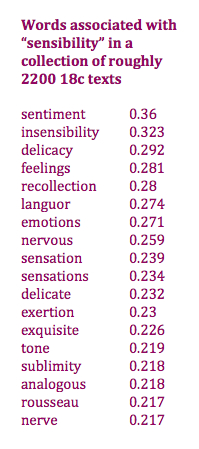
We could certainly model literary taste. We trained a model to distinguish poets reviewed in elite literary magazines from a less celebrated “contrast group” selected randomly. The model achieved roughly 79% accuracy, 1820-1919, and the stability of the model itself raised interesting questions. But we didn’t find that the model’s accuracy increased across time in the way we would have expected in a period when elite and popular literary taste are specializing and growing apart.

Instead of concluding that the division never happened, we guessed that we had misunderstood it or looked in the wrong place. Algee-Hewitt and McGurl have pretty decisively confirmed that a divide exists in the twentieth century. So we ought to be able to see it emerging. Maybe we needed to reach further into the twentieth century — or maybe we would have better luck with fiction, since the history of fiction provides evidence about sales, as well as prestige?

In fact, getting evidence about that second, economic axis seems to be the key. It took work by many hands over a couple of years: Kyle Johnston, Sabrina Lee, and Jessica Mercado, as well as Jordan Sellers, have all contributed to this project. I’m presenting a preliminary account of our results at Cultural Analytics 2017, and this blog post is just a brief summary of the main point.

When you look at the books described as bestsellers by Publisher’s Weekly, or by book historians (see references to Altick, Bloom, Hackett, Leavis, below) it’s easy to see the two circles of the Venn diagram pulling apart: on the one hand bestsellers, on the other hand books reviewed in elite venues. (For our definition of “elite venues” see the “Table” in a supporting code & data repository.)

$authorfractions2$

On the other hand, when you back up from bestsellers to look at a broader sample of literary production, it’s still not easy to detect increasing stylistic differentiation between the elite “reviewed” texts and the rest of the literary field. A classifier trained on the reviewed fiction has roughly 72.5% accuracy from 1850 to 1949; if you break the century into parts, there are some variations in accuracy, but no consistent pattern. (In a subsequent blog post, I’ll look at the fiddly details of algorithm choice and feature engineering, but the long and short of that question is — it doesn’t make a significant difference.)

To understand why the growing separation of bestsellers from “reviewed” texts at the high end of the market doesn’t seem to make literary production as a whole more strongly stratified, I’ve tried mapping authors onto a two-dimensional model of the literary field, intended to echo Pierre Bourdieu’s well-known diagrams of the interaction between economic and cultural distinction.

Pierre Bourdieu, The Field of Cultural Production (1993), p. 49.

In the diagram below, for instance, the horizontal axis represents sales, and the vertical axis represents prestige. Sales would be easy to measure, if we had all the data. We actually don’t — so see the end of this post for the estimation strategy I adopted. Prestige, on the other hand, is difficult to measure: it’s perspectival and complex. So we modeled prestige by sampling texts that were reviewed in prominent literary magazines, and then training a model that used textual cues to predict the probability that any given book came from the “reviewed” set. An author’s prestige in this diagram is simply the average probability of review for their books. (The Stanford Literary Lab has similarly recreated Bourdieu’s model of distinction in their pamphlet “Canon/Archive,” using academic citations as a measure of prestige.)

The upward drift of these points reveals a fairly strong correlation between prestige and sales. It is possible to find a few high-selling authors who are predicted to lack critical prestige — notably, for instance, the historical novelist W. H. Ainsworth and the sensation novelist Ellen Wood, author of East Lynne. It’s harder to find authors who have prestige but no sales: there’s not much in the northwest corner of the map. Arthur Helps, a Cambridge Apostle, is a fairly lonely figure.

Fast-forward seventy-five years and we see a different picture.

The correlation between sales and prestige is now weaker; the cloud of authors is “rounder” overall.

There are also more authors in the “upper midwest” portion of the map now — people like Zora Neale Hurston and James Joyce, who have critical prestige but not enormous sales (or not up to 1949, at least as far as my model is aware).

There’s also a distinct “genre fiction” and “pulp fiction” world emerging in the southeast corner of this map, ranging from Agatha Christie to Mickey Spillane. (A few years earlier, Edgar Rice Burroughs and Zane Gray are in the same region.)

Moreover, if you just look at the large circles (the authors we’re most likely to remember), you can start to see how people in this period might get the idea that sales are actually negatively correlated with critical prestige. The right side of the map almost looks like a diagonal line slanting down from William Faulkner to P. G. Wodehouse.

That negative correlation doesn’t really characterize the field as a whole. Critical prestige still has a faint positive correlation with sales, as people over on the left side of the map might sadly remind us. But a brief survey of familiar names could give you the opposite impression.

In short, we’re not necessarily seeing a stronger stratification of the literary field. The change might better be described as a decline in the correlation of two existing forms of distinction. And as they become less correlated, the difference between them becomes more visible, especially among the well-known names on the right side of the map.

So, while we’re broadly confirming an existing story about literary history, the evidence also suggests that the metaphor of a “great divide” is a bit of an exaggeration. We don’t see any chasm emerging.

Maps of the literary field also help me understand why a classifier trained on an elite “reviewed” sample didn’t necessarily get stronger over time. The correlation of prestige and sales in the Victorian era means that the line separating the red and blue samples was strongly tilted there, and may borrow some of its strength from both axes. (It’s really a boundary between the prominent and the obscure.)

As we move into the twentieth century, the slope of the line gets flatter, and we get closer to a “pure” model of prestige (as distinguished from sales). But the boundary itself may not grow more clearly marked, if you’re sampling a group of the same size. (However, if you leave The New Republic and New Yorker behind, and sample only works reviewed in little magazines, you do get a more tightly unified group of texts that can be distinguished from a random sample with 83% accuracy.)

This is all great, you say — but how exactly are you “estimating” sales? We don’t actually have good sales figures for every author in HathiTrust Digital Library; we have fairly patchy records that depend on individual publishers.

For the answer to that question, I’m going to refer you to the github repo where I work out a model of sales. The short version is that I borrow a version of “empirical Bayes” from Julia Silge and David Robinson, and apply it to evidence drawn from bestseller lists as well as digital libraries, to construct a rough estimate of each author’s relative prominence in the market. The trick is, basically, to use the evidence we have to construct an estimate of our uncertainty, and then use our uncertainty to revise the evidence. The picture on the left gives you a rough sense of how that transformation works. I think empirical Bayes may turn out to be useful for a lot of problems where historians need to reconstruct evidence that is patchy or missing in the historical record, but the details are too much to explain here; see Silge’s post and my Jupyter notebook.

Bubble charts invite mouse-over exploration. I can’t easily embed interactive viz in this blog, but here are a few links to plotly visualizations:

https://plot.ly/~TedUnderwood/8/the-literary-field-1850-1874/

https://plot.ly/~TedUnderwood/4/the-literary-field-1875-1899/

https://plot.ly/~TedUnderwood/2/the-literary-field-1900-1924/

https://plot.ly/~TedUnderwood/6/the-literary-field-1925-1949/

Acknowledgments

The texts used here are drawn from HathiTrust via the HathiTrust Research Center. Parts of the research were funded by the Andrew G Mellon Foundation via the WCSA+DC grant, and part by SSHRC via NovelTM.

Most importantly, I want to acknowledge my collaborators on this project, Kyle Johnston, Sabrina Lee, Jessica Mercado, and Jordan Sellers. They contributed a lot of intellectual depth to the project — for instance by doing research that helped us decide which periodicals should represent a given period of literary history.

References

Algee-Hewitt, Mark, and Mark McGurl. “Between Canon and Corpus: Six Perspectives on 20th-Century Novels.” Stanford Literary Lab, Pamphlet 9, 2015. https://litlab.stanford.edu/LiteraryLabPamphlet8.pdf

Algee-Hewitt, Mark, Sarah Allison, Marissa Gemma, Ryan Heuser, Franco Moretti, Hannah Walser. “Canon/Archive: Large-Scale Dynamics in the Literary Field.” Stanford Literary Lab, January 2016. https://litlab.stanford.edu/LiteraryLabPamphlet11.pdf

Altick, Richard D. The English Common Reader: A Social History of the Mass Reading Public 1800-1900. Chicago: University of Chicago Press, 1957.

Bloom, Clive. Bestsellers: Popular Fiction Since 1900. 2nd edition. Houndmills: Palgrave Macmillan, 2008.

Hackett, Alice Payne, and James Henry Burke. 80 Years of Best Sellers 1895-1975. New York: R.R. Bowker, 1977.

Leavis, Q. D. Fiction and the Reading Public. 1935.

Mott, Frank Luther. Golden Multitudes: The Story of Bestsellers in the United States. New York: R. R. Bowker, 1947.

Robinson, David. Introduction to Empirical Bayes: Examples from Baseball Statistics. 2017. http://varianceexplained.org/r/empirical-bayes-book/

Silge, Julia. “Singing the Bayesian Beginner Blues.” data science ish, September 2016. http://juliasilge.com/blog/Bayesian-Blues/

Unsworth, John. 20th Century American Bestsellers. (http://bestsellers.lib.virginia.edu)

20c pace of historical change statistics

You say you found a revolution.

Post author By tedunderwood
Post date February 7, 2016
1 Comment on You say you found a revolution.

by Ted Underwood, Hoyt Long, Richard Jean So, and Yuancheng Zhu

This is the second part of a two-part blog post about quantitative approaches to cultural change, focusing especially on a recent article that claimed to identify “stylistic revolutions” in popular music.

Although “The Evolution of Popular Music” (Mauch et al.) appeared in a scientific journal, it raises two broad questions that humanists should care about:

Are measures of the stylistic “distance” between songs or texts really what we mean by cultural change?
If we did take that approach to measuring change, would we find brief periods where the history of music or literature speeds up by a factor of six, as Mauch et al. claim?

Underwood’s initial post last October discussed both of these questions. The first one is more important. But it may also be hard to answer — in part because “cultural change” could mean a range of different things (e.g., the ever-finer segmentation of the music market, not just changes that affect it as a whole).

So putting the first question aside for now, let’s look at the the second one closely. When we do measure the stylistic or linguistic “distance” between works of music or literature, do we actually discover brief periods of accelerated change?

The authors of “The Evolution of Popular Music” say “yes!” Epochal breaks can be dated to particular years.

We identified three revolutions: a major one around 1991 and two smaller ones around 1964 and 1983 (figure 5b). From peak to succeeding trough, the rate of musical change during these revolutions varied four- to six-fold.

Tying musical revolutions to particular years (and making 1991 more important than 1964) won the article a lot of attention in the press. Underwood’s questions about these claims last October stirred up an offline conversation with three researchers at the University of Chicago, who have joined this post as coauthors. After gathering in Hyde Park to discuss the question for a couple of days, we’ve concluded that “The Evolution of Popular Music” overstates its results, but is also a valuable experiment, worth learning from. The article calculates significance in a misleading way: only two of the three “revolutions” it reported are really significant at p < 0.05, and it misses some odd periods of stasis that are just as significant as the periods of acceleration. But these details are less interesting than the reason for the error, which involved a basic challenge facing quantitative analysis of history.

To explain that problem, we’ll need to explain the central illustration in the original article. The authors’ strategy was to take every quarter-year of the Billboard Hot 100 between 1960 and 2010, and compare it to every other quarter, producing a distance matrix where light (yellow-white) colors indicate similarity, and dark (red) colors indicate greater differences. (Music historians may wonder whether “harmonic and timbral topics” are the right things to be comparing in the first place, and it’s a fair question — but not central to our purpose in this post, so we’ll give it a pass.)

You see a diagonal white line in the matrix, because comparing a quarter to itself naturally produces a lot of similarity. As you move away from that line (to the upper left or lower right), you’re making comparisons across longer and longer spans of time, so colors become darker (reflecting greater differences).

Figure 5 from Mauch, et. al., “The evolution of popular music” (RSOS 2015).

Then, underneath the distance matrix, Mauch et al. provide a second illustration that measures “Foote novelty” for each quarter. This is a technique for segmenting audio files developed by Jonathan Foote. The basic idea is to look for moments of acceleration where periods of relatively slow change are separated by a spurt of rapid change. In effect, that means looking for a point where yellow “squares” of similarity touch at their corners.

For instance, follow the dotted line associated with 1991 in the illustration above up to its intersection with the white diagonal. At that diagonal line, 1991 is (unsurprisingly) similar to itself. But if you move upward in the matrix (comparing 1991 to its own future), you rapidly get into red areas, revealing that 1994 is already quite different. The same thing is true if you move over a year to 1992 and then move down (comparing 1992 to its own past). At a “pinch point” like this, change is rapid. According to “The Evolution of Popular Music,” we’re looking at the advent of rap and hip-hop in the Billboard Hot 100. Contrast this pattern, for instance, to a year like 1975, in the middle of a big yellow square, where it’s possible to move several years up or down without encountering significant change.

Mathematically, “Foote novelty” is measured by sliding a smaller matrix along the diagonal timeline, multiplying it element-wise with the measurements of distance underlying all those red or yellow points. Then you add up the multiplied values. The smaller matrix has positive and negative coefficients corresponding to the “squares” you want to contrast, as seen on the right.

As you can see, matrices of this general shape will tend to produce a very high sum when they reach a pinch point where two yellow squares (of small distances) are separated by the corners of reddish squares (containing large distances) to the upper left and lower right. The areas of ones and negative-ones can be enlarged to measure larger windows of change.

This method works by subtracting the change on either side of a temporal boundary from the changes across the boundary itself. But it has one important weakness. The contrast between positive and negative areas in the matrix is not apples-to-apples, because comparisons made across a boundary are going to stretch across a longer span of time, on average, than the comparisons made within the half-spans on either side. (Concretely, you can see that the ones in the matrix above will be further from the central diagonal timeline than the negative-ones.)

If you’re interested in segmenting music, that imbalance may not matter. There’s a lot of repetition in music, and it’s not always true that a note will resemble a nearby note more than it resembles a note from elsewhere in the piece. Here’s a distance matrix, for instance, from The Well-Tempered Clavier, used by Foote as an example.

From Foote, “Automatic Audio Segmentation Using a Measure of Audio Novelty.”

Unlike the historical matrix in “The Evolution of Popular Music,” this has many light spots scattered all over — because notes are often repeated.

Original distance matrix produced using data from Mauch et al. (2015).

History doesn’t repeat itself in the same way. It’s extremely likely (almost certain) that music from 1992 will resemble music from 1991 more than it resembles music from 1965. That’s why the historical distance matrix has a single broad yellow path running from lower left to upper right.

As a result, historical sequences are always going to produce very high measurements of Foote novelty. Comparisons across a boundary will always tend to create higher distances than the comparisons within the half-spans on either side, because differences across longer spans of time always tend to be bigger.

Matrix produced by permuting years and then measuring the distances between them.

This also makes it tricky to assess the significance of “Foote novelty” on historical evidence. You might ordinarily do this using a “permutation test.” Scramble all the segments of the timeline repeatedly and check Foote novelty each time, in order to see how often you get “squares” as big or well-marked as the ones you got in testing the real data. But that sort of scrambling will make no sense at all when you’re looking at history. If you scramble the years, you’ll always get a matrix that has a completely different structure of similarity — because it’s no longer sequential.

The Foote novelties you get from a randomized matrix like this will always be low, because “Foote novelty” partly measures the contrast between areas close to, and far from, the diagonal line (a contrast that simply doesn’t exist here).

This explains a deeply puzzling aspect of the original article. If you look at the significance curves labeled .001, .01, and 0.05 in the visualization of Foote novelties (above), you’ll notice that every point in the original timeline had a strongly significant novelty score. As interpreted by the caption, this seems to imply that change across every point was faster than average for the sequence … which … can’t possibly be true everywhere.

All this image really reveals is that we’re looking at evidence that takes the form of a sequential chain. Comparisons across long spans of time always involve more difference than comparisons across short ones — to an extent that you would never find in a randomized matrix.

In short, the tests in Mauch et al. don’t prove that there were significant moments of acceleration in the history of music. They just prove that we’re looking at historical evidence! The authors have interpreted this as a sign of “revolution,” because all change looks revolutionary when compared to temporal chaos.

On the other hand, when we first saw the big yellow and red squares in the original distance matrix, it certainly looked like a significant pattern. Granted that the math used in the article doesn’t work — isn’t there some other way to test the significance of these variations?

It took us a while to figure out, but there is a reliable way to run significance tests for Foote novelty. Instead of scrambling the original data, you need to permute the distances along diagonals of the distance matrix.

Produced by permuting diagonals in the original matrix.

In other words, you take a single diagonal line in the original matrix and record the measurements of distance along that line. (If you’re looking at the central diagonal, this will contain a comparison of every quarter to itself; if you move up one notch, it will contain a comparison of every quarter to the quarter in its immediate future.) Then you scramble those values randomly, and put them back on the same line in the matrix. (We’ve written up a Jupyter notebook showing how to do it.) This approach distributes change randomly across time while preserving the sequential character of the data: comparisons over short spans of time will still tend to reveal more similarity than long ones.

If you run this sort of permutation 100 times, you can discover the maximum and minimum Foote novelties that would be likely to occur by chance.

Measurements of Foote novelty produced by a matrix with a five-year half-width, and the thresholds for significance.

Variation between the two red lines isn’t statistically significant — only the peaks of rapid change poking above the top line, and the troughs of stasis dipping below the bottom line. (The significance of those troughs couldn’t become visible in the original article, because the question had been framed in a way that made smaller-than-random Foote novelties impossible by definition.)

These corrected calculations do still reveal significant moments of acceleration in the history of the Billboard Hot 100: two out of three of the “revolutions” Mauch et al. report (around 1983 and 1991) are still significant at p < 0.05 and even p < 0.001. (The British Invasion, alas, doesn’t pass the test.) But the calculations also reveal something not mentioned in the original article: a very significant slowing of change after 1995.

Can we still call the moments of acceleration in this graph stylistic “revolutions”?

Foote novelty itself won’t answer the question. Instead of directly measuring a rate of change, it measures a difference between rates of change in overlapping periods. But once we’ve identified the periods that interest us, it’s simple enough to measure the pace of change in each of them. You can just divide the period in half and compare the first half to the second (see the “Effect size” section in our Jupyter notebook). This confirms the estimate in Mauch et al.: if you compare the most rapid period of change (from 1990 to 1994) to the slowest four years (2001 to 2005), there is a sixfold difference between them.

On the other hand, it could be misleading to interpret this as a statement about the height of the early-90s “peak” of change, since we’re comparing it to an abnormally stable period in the early 2000s. If we compare both of those periods to the mean rate of change across any four years in this dataset, we find that change in the early 90s was about 171% of the mean pace, whereas change in the early 2000s was only 29% of mean. Proportionally, the slowing of change after 1995 might be the more dramatic aberration here.

Overall, the picture we’re seeing is different from the story in “The Evolution of Popular Music.” Instead of three dramatic “revolutions” dated to specific years, we see two periods where change was significantly (but not enormously) faster than average, and two periods where it was slower. These periods range from four to fifteen years in length.

Humanists will surely want to challenge this picture in theoretical ways as well. Was the Billboard Hot 100 the right sample to be looking at? Are “timbral topics” the right things to be comparing? These are all valid questions.

But when scientists make quantitative claims about humanistic subjects, it’s also important to question the quantitative part of their argument. If humanists begin by ceding that ground, the conversation can easily become a stalemate where interpretive theory faces off against the (supposedly objective) logic of science, neither able to grapple with the other.

One of the authors of “The Evolution of Popular Music,” in fact, published an editorial in The New York Times representing interdisciplinary conversation as exactly this sort of stalemate between “incommensurable interpretive fashions” and the “inexorable logic” of math (“One Republic of Learning,” NYT Feb 2015). But in reality, as we’ve just seen, the mathematical parts of an argument about human culture also encode interpretive premises (assumptions, for instance, about historical difference and similarity). We need to make those premises explicit, and question them.

Having done that here, and having proposed a few corrections to “The Evolution of Popular Music,” we want to stress that the article still seems to us a bold and valuable experiment that has advanced conversation about cultural history. The basic idea of calculating “Foote novelty” on a distance matrix is useful: it can give historians a way of thinking about change that acknowledges several different scales of comparison at once.

The authors also deserve admiration for making their data available; that transparency has permitted us to replicate and test their claims, just as Andrew Goldstone recently tested Ted Underwood’s model of poetic prestige, and Annie Swafford tested Matt Jockers’ syuzhet package. Our understanding of these difficult problems can only advance through collective practices of data-sharing and replication. Being transparent in our methods is more important, in the long run, than being right about any particular detail.

The authors want to thank the NovelTM project for supporting the collaboration reported here. (And we promise to apply these methods to the history of the novel next.)

References:

Jonathan Foote. Automatic audio segmentation using a measure of audio novelty. In Proceedings of IEEE International Conference on Multimedia and Expo, vol. I, pp. 452-455, 2000.

Mauch et al. 2015. “The Evolution of Popular Music.” Royal Society Open Science. May 6, 2015. DOI: 10.1098/rsos.150081

Postscript: Several commenters on the original blog post proposed simpler ways of measuring change that begin by comparing adjacent segments of a timeline. This an intuitive approach, and a valid one, but it does run into difficulties — as we discovered when we tried to base changepoint analysis on it (Jupyter notebook here). The main problem is that apparent trajectories of change can become very delicately dependent on the particular window of comparison you use. You’ll see lots of examples of that problem toward the end of our notebook.

The advantage of the “Foote novelty” approach is that it combines lots of different scales of comparison (since you’re considering all the points in a matrix — some closer and some farther from the timeline). That makes the results more robust. Here, for instance, we’ve overlaid the “Foote novelties” generated by three different windows of comparison on the music dataset, flagging the quarters that are significant at p < 0.05 in each case.

This sort of close congruence is not something we found with simpler methods. Compare the analogous image below, for instance. Part of the chaos here is a purely visual issue related to the separation of curves — but part comes from using segments rather than a distance matrix.

historicism math methodology pace of historical change

Can we date revolutions in the history of literature and music?

Post author By tedunderwood
Post date October 3, 2015
18 Comments on Can we date revolutions in the history of literature and music?

Humanists know the subjects we study are complex. So on the rare occasions when we describe them with numbers at all, we tend to proceed cautiously. Maybe too cautiously. Distant readers have spent a lot of time, for instance, just convincing colleagues that it might be okay to use numbers for exploratory purposes.

But the pace of this conversation is not entirely up to us. Outsiders to our disciplines may rush in where we fear to tread, forcing us to confront questions we haven’t faced squarely.

For instance, can we use numbers to identify historical periods when music or literature changed especially rapidly or slowly? Humanists have often used qualitative methods to make that sort of argument. At least since the nineteenth century, our narratives have described periods of stasis separated by paradigm shifts and revolutionary ruptures. For scientists, this raises an obvious, tempting question: why not actually measure rates of change and specify the points on the timeline when ruptures happened?

The highest-profile recent example of this approach is an article in Royal Society Open Science titled “The evolution of popular music” (Mauch et al. 2015). The authors identify three moments of rapid change in US popular music between 1960 and 2010. Moreover, they rank those moments, and argue that the advent of rap caused popular music to change more rapidly than the British Invasion — a claim you may remember, because it got a lot of play in the popular press. Similar arguments have appeared about the pace of change in written expression — e.g, a recent article argues that 1917 was a turning point in political rhetoric (h/t Cameron Blevins).

When disciplinary outsiders make big historical claims, humanists may be tempted just to roll our eyes. But I don’t think this is a kind of intervention we can afford to ignore. Arguments about the pace of cultural change engage theoretical questions that are fundamental to our disciplines, and questions that genuinely fascinate the public. If scientists are posing these questions badly, we need to explain why. On the other hand, if outsiders are addressing important questions with new methods, we need to learn from them. Scholarship is not a struggle between disciplines where the winner is the discipline that repels foreign ideas with greatest determination.

I feel particularly obligated to think this through, because I’ve been arguing for a couple of years that quantitative methods tend to reveal gradual change rather than the sharply periodized plateaus we might like to discover in the past. But maybe I just haven’t been looking closely enough for discontinuities? Recent articles introduce new ways of locating and measuring them.

This blog post applies methods from “The evolution of popular music” to a domain I understand better — nineteenth-century literary history. I’m not making a historical argument yet, just trying to figure out how much weight these new methods could actually support. I hope readers will share their own opinions in the comments. So far I would say I’m skeptical about these methods — or at least skeptical that I know how to interpret them.

How scientists found musical revolutions.

Mauch et al. start by collecting thirty-second snippets of songs in the Billboard Hot 100 between 1960 and 2010. Then they topic-model the collection to identify recurring harmonic and timbral topics. To study historical change, they divide the fifty-year collection into two hundred quarter-year periods, and aggregate the topic frequencies for each quarter. They’re thus able to create a heat map of pairwise “distances” between all these quarter-year periods. This heat map becomes the foundation for the crucial next step in their argument — the calculation of “Foote novelty” that actually identifies revolutionary ruptures in music history.

Figure 5 from Mauch, et. al., “The evolution of popular music” (RSOS 2015).

The diagonal line from bottom left to top right of the heat map represents comparisons of each time segment to itself: that distance, obviously, should be zero. As you rise above that line, you’re comparing the same moment to quarters in its future; if you sink below, you’re comparing it to its past. Long periods where topic distributions remain roughly similar are visible in this heat map as yellowish squares. (In the center of those squares, you can wander a long way from the diagonal line without hitting much dissimilarity.) The places where squares are connected at the corners are moments of rapid change. (Intuitively, if you deviate to either side of the narrow bridge there, you quickly get into red areas. The temporal “window of similarity” is narrow.) Using an algorithm outlined by Jonathan Foote (2000), the authors translate this grid into a line plot where the dips represent musical “revolutions.”

Trying the same thing on the history of the novel.

Could we do the same thing for the history of fiction? The labor-intensive part would be coming up with a corpus. Nineteenth-century literary scholars don’t have a Billboard Hot 100. We could construct one, but before I spend months crafting a corpus to address this question, I’d like to know whether the question itself is meaningful. So this is a deliberately rough first pass. I’ve created a sample of roughly 1000 novels in a quick and dirty way by randomly selecting 50 male and 50 female authors from each decade 1820-1919 in HathiTrust. Each author is represented in the whole corpus only by a single volume. The corpus covers British and American authors; spelling is normalized to modern British practice. If I were writing an article on this topic I would want a larger dataset and I would definitely want to record things like each author’s year of birth and nationality. This is just a first pass.

Because this is a longer and sparser sample than Mauch et al. use, we’ll have to compare two-year periods instead of quarters of a year, giving us a coarser picture of change. It’s a simple matter to run a topic model (with 50 topics) and then plot a heat map based on cosine similarities between the topic distributions in each two-year period.

Heatmap and Foote novelty for 1000 novels, 1820-1919. Rises in the trend lines correspond to increased Foote novelty.

Voila! The dark and light patterns are not quite as clear here as they are in “The evolution of popular music.” But there are certainly some squarish areas of similarity connected at the corners. If we use Foote novelty to interpret this graph, we’ll have one major revolution in fiction around 1848, and a minor one around 1890. (I’ve flipped the axis so peaks, rather than dips, represent rapid change.) Between these peaks, presumably, lies a valley of Victorian stasis.

Is any of that true? How would we know? If we just ask whether this story fits our existing preconceptions, I guess we could make it fit reasonably well. As Eleanor Courtemanche pointed out when I discussed this with her, the end of the 1840s is often understood as a moment of transition to realism in British fiction, and the 1890s mark the demise of the three-volume novel. But it’s always easy to assimilate new evidence to our preconceptions. Before we rush to do it, let’s ask whether the quantitative part of this argument has given us any reason at all to believe that the development of English-language fiction really accelerated in the 1840s.

I want to pose four skeptical questions, covering the spectrum from fiddly quantitative details to broad theoretical doubts. I’ll start with the fiddliest part.

1) Is this method robust to different ways of measuring the “distance” between texts?

The short answer is “yes.” The heat maps plotted above are calculated on a topic model, after removing stopwords, but I get very similar results if I compare texts directly, without a topic model, using a range of different distance metrics. Mauch et al. actually apply PCA as well as a topic model; that doesn’t seem to make much difference. The “moments of revolution” stay roughly in the same place.

2) How crucial is the “Foote novelty” piece of the method?

Very crucial, and this is where I think we should start to be skeptical. Mauch et al. are identifying moments of transition using a method that Jonathan Foote developed to segment audio files. The algorithm is designed to find moments of transition, even if those moments are quite subtle. It achieves this by making comparisons — not just between the immediately previous and subsequent moments in a stream of observations — but between all segments of the timeline.

It’s a clever and sensitive method. But there are other, more intuitive ways of thinking about change. For instance, we could take the first ten years of the dataset as a baseline and directly compare the topic distributions in each subsequent novel back to the average distribution in 1820-1829. Here’s the pattern we see if we do that:

That looks an awful lot like a steady trend; the trend may gradually flatten out (either because change really slows down or, more likely, because cosine distances are bounded at 1.0) but significant spurts of revolutionary novelty are in any case quite difficult to see here.

That made me wonder about the statistical significance of “Foote novelty,” and I’m not satisfied that we know how to assess it. One way to test the statistical significance of a pattern is to randomly permute your data and see how often patterns of the same magnitude turn up. So I repeatedly scrambled the two-year periods I had been comparing, constructed a heat matrix by comparing them pairwise, and calculated Foote novelty.

A heatmap produced by randomly scrambling the fifty two-year periods in the corpus. The “dates” on the timeline are now meaningless.

When I do this I almost always find Foote novelties that are as large as the ones we were calling “revolutions” in the earlier graph.

The authors of “The evolution of popular music” also tested significance with a permutation test. They report high levels of significance (p < 0.01) and large effect sizes (they say music changes four to six times faster at the peak of a revolution than at the bottom of a trough). Moreover, they have generously made their data available, in a very full and clearly-organized csv. But when I run my permutation test on their data, I run into the same problem — I keep discovering random Foote novelties that seem as large as the ones in the real data.

It’s possible that I’m making some error, or that we're testing significance differently. I'm permuting the underlying data, which always gives me a matrix that has the checkerboardy look you see above. The symmetrical logic of pairwise comparison still guarantees that random streaks organize themselves in a squarish way, so there are still “pinch points” in the matrix that create high Foote novelties. But the article reports that significance was calculated “by random permutation of the distance matrix.” If I actually scramble the rows or columns of the distance matrix itself I get a completely random pattern that does give me very low Foote novelty scores. But I would never get a pattern like that by calculating pairwise distances in a real dataset, so I haven’t been able to convince myself that it’s an appropriate test.

3) How do we know that all forms of change should carry equal cultural weight?

Now we reach some questions that will make humanists feel more at home. The basic assumption we’re making in the discussion above is that all the features of an expressive medium bear historical significance. If writers replace “love” with “spleen,” or replace “cannot” with “can’t,” it may be more or less equal where this method is concerned. It all potentially counts as change.

This is not to say that all verbal substitutions will carry exactly equal weight. The weight assigned to words can vary a great deal depending on how exactly you measure the distance between texts; topic models, for instance, will tend to treat synonyms as equivalent. But — broadly speaking — things like contractions can still potentially count as literary change, just as instrumentation and timbre count as musical change in “The evolution of popular music.”

At this point a lot of humanists will heave a relieved sigh and say “Well! We know that cultural change doesn’t depend on that kind of merely verbal difference between texts, so I can stop worrying about this whole question.”

Not so fast! I doubt that we know half as much as we think we know about this, and I particularly doubt that we have good reasons to ignore all the kinds of change we’re currently ignoring. Paying attention to merely verbal differences is revealing some massive changes in fiction that previously slipped through our net — like the steady displacement of abstract social judgment by concrete description outlined by Heuser and Le-Khac in LitLab pamphlet #4.

For me, the bottom line is that we know very little about the kinds of change that should, or shouldn’t, count in cultural history. “The evolution of popular music” may move too rapidly to assume that every variation of a waveform bears roughly equal historical significance. But in our daily practice, literary historians rely on a set of assumptions that are much narrower and just as arbitrary. An interesting debate could take place about these questions, once humanists realize what’s at stake, but it’s going to be a thorny debate, and it may not be the only way forward, because …

4) Instead of discussing change in the abstract, we might get further by specifying the particular kinds of change we care about.

Our systems of cultural periodization tend to imply that lots of different aspects of writing (form and style and theme) all change at the same time — when (say) “aestheticism” is replaced by “modernism.” That underlying theory justifies the quest for generalized cultural growth spurts in “The evolution of popular music.”

But we don’t actually have to think about change so generally. We could specify particular social questions that interest us, and measure change relative to those questions.

The advantage of this approach is that you no longer have to start with arbitrary assumptions about the kind of “distance” that counts. Instead you could use social evidence to train a predictive model. Insofar as that model predicts the variables you care about, you know that it’s capturing the specific kind of change that matters for your question.

Jordan Sellers and I took this approach in a working paper we released last spring, modeling the boundary between volumes of poetry that were reviewed in prominent venues, and those that remained obscure. We found that the stylistic signals of poetic prestige remained relatively stable across time, but we also found that they did move, gradually, in a coherent direction. What we didn’t do, in that article, is try to measure the pace of change very precisely. But conceivably you could, using Foote novelty or some other method. Instead of creating a heatmap that represents pairwise distances between texts, you could create a grid where models trained to recognize a social boundary in particular decades make predictions about the same boundary in other decades. If gender ideologies or definitions of poetic prestige do change rapidly in a particular decade, it would show up in the grid, because models trained to predict authorial gender or poetic prominence before that point would become much worse at predicting it afterward.

Conclusion

I haven’t come to any firm conclusion about “The evolution of popular music.” It’s a bold article that proposes and tests important claims; I’ve learned a lot from trying the same thing on literary history. I don’t think I proved that there aren’t any revolutionary growth spurts in the history of the novel. It’s possible (my gut says, even likely) that something does happen around 1848 and around 1890. But I wasn’t able to show that there’s a statistically significant acceleration of change at those moments. More importantly, I haven’t yet been able to convince myself that I know how to measure significance and effect size for Foote novelty at all; so far my attempts to do that produce results that seem different from the results in a paper written by four authors who have more scientific training than I do, so there’s a very good chance that I’m misunderstanding something.

I would welcome comments, because there are a lot of open questions here. The broader task of measuring the pace of cultural change is the kind of genuinely puzzling problem that I hope we’ll be discussing at more length in the IPAM Cultural Analytics workshop next spring at UCLA.

Postscript Oct 5: More will be coming in a day or two. The suggestions I got from comments (below) have helped me think the quantitative part of this through, and I’m working up an iPython notebook that will run reliable tests of significance and effect size for the music data in Mauch et al. as well as a larger corpus of novels. I have become convinced that significance tests on Foote novelty are not a good way to identify moments of rapid change. The basic problem with that approach is that sequential datasets will always have higher Foote novelties than permuted (non-sequential) datasets, if you make the “window” wide enough — even if the pace of change remains constant. Instead, borrowing an idea from Hoyt Long and Richard So, I’m going to use a Chow test to see whether rates of change vary.

Postscript Oct 8: Actually it could be a while before I have more to say about this, because the quantitative part of the problem turns out to be hard. Rates of change definitely vary. Whether they vary significantly, may be a tricky question.

References:

Jonathan Foote. Automatic audio segmentation using a measure of audio novelty. In Proceedings of IEEE International Conference on Multimedia and Expo, vol. I, pp. 452-455, 2000.

Matthias Mauch, Robert M. MacCallum, Mark Levy, Armand M. Leroi. The evolution of popular music. Royal Society Open Science. May 6, 2015.

Tags fiction, literature, statistics

interpretive theory statistics

Do humanists get their ideas from anything at all?

Post author By tedunderwood
Post date January 24, 2012
11 Comments on Do humanists get their ideas from anything at all?

My reaction to Stanley Fish’s third column on digital humanities was at first so negative that I thought it not worth writing about. But in the light of morning, there is something here worth discussing. Fish raises a neglected issue that I (and a bunch of other people cited at the end of this post) have been trying to foreground: the role of discovery in the humanities. He raises the issue symptomatically, by suppressing it, but the problem is too important to let that slide.

Fish argues, in essence, that digital humanists let the data suggest hypotheses for them instead of framing hypotheses that are then tested against evidence.

The usual way of doing this is illustrated by my example: I began with a substantive interpretive proposition … and, within the guiding light, indeed searchlight, of that proposition I noticed a pattern that could, I thought be correlated with it. I then elaborated the correlation.

The direction of my inferences is critical: first the interpretive hypothesis and then the formal pattern, which attains the status of noticeability only because an interpretation already in place is picking it out.

The direction is the reverse in the digital humanities: first you run the numbers, and then you see if they prompt an interpretive hypothesis. The method, if it can be called that, is dictated by the capability of the tool.

The underlying element of truth here is that all researchers — humanists and scientists alike — do need to separate the process of discovering a hypothesis from the process of testing it. Otherwise you run into what we unreflecting empiricists call “the problem of data dredging.” If you simply sweep a net through an ocean of data, and frame a conclusion based on whatever you catch, you’re not properly testing anything, because you’re implicitly testing an infinite number of hypotheses that are left unstated — and the significance of any single test is reduced when it’s run as part of a large battery.

That’s true, but it’s also a problem that people who do data mining are quite self-conscious about. It’s why I never stop linking to this xkcd comic about “significance.” And it’s why Matt Wilkens (mistargeted by Fish as an emblem of this interpretive sin) goes through a deliberately iterative process of first framing hypotheses about nineteenth-century geographical imagination and then testing them. (For instance, after noticing that certain states seem especially prominent in 19c American fiction, he tests whether this remains true after you compensate for differences in population size, and then proposes a pair of hypotheses that he suggests will need to be evaluated against additional “test cases.”)

Satan_Sin_Death — Wiliam Blake, "Satan, Sin, and Death"

More importantly, Fish profoundly misrepresents his own (traditional) interpretive procedure by pretending that the act of interpretation is wholly contained in a single encounter with evidence. On his account we normally begin with a hypothesis (which seems to have sprung, like Sin, fully-formed from our head), and test it against a single sentence.

In reality, of course, our “interpretive proposition” is often suggested by the same evidence that confirms it. Or — more commonly — we derive a hypothesis from one example, and then read patiently through dozens of books until we have gathered enough confirming evidence to write a chapter. This process runs into a different interpretive fallacy: if you keep testing a hypothesis until you’ve confirmed it, you’re not testing it at all. And it’s a bit worse than that, because in practice what we do now is go to a full-text search engine and search for terms that would go together if our assumptions were correct. (In the example Fish offers, this might be “bishops” and “presbyters.”) If you find three sentences where those terms coincide, you’ve got more than enough evidence to prop up an argument, using our richly humanistic (cough, anecdotal) conception of evidence. And of course a full-text search engine can find you three examples of just about anything. But we don’t have to worry about this, because search engines are not tools that dictate a method; they are transparent extensions of our interpretive sensibility.

The basic mistake that Fish is making is this: he pretends that humanists have no discovery process at all. For Fish, the interpretive act is always fully contained in an encounter with a single piece of evidence. How your “interpretive proposition” got framed in the first place is a matter of no consequence: some readers are just fortunate to have propositions that turn out to be correct. Fish is not alone in this idealized model of interpretation; it’s widespread among humanists.

Fish is resisting the assistance of digital techniques, not because they would impose scientism on the humanities, but because they would force us to acknowledge that our ideas do after all come from somewhere — whether a search engine or a commonplace book. But as Peter Stallybrass eloquently argued five years ago in PMLA (h/t Mark Sample) the process of discovery has always been collaborative, and has long — at least since early modernity — been embodied in specific textual technologies.

References
Stallybrass, Peter. “Against Thinking.” PMLA 122.5 (2007): 1580-1587.
Wilkens, Matthew. “Geolocation Extraction and Mapping of Nineteenth-Century U.S. Fiction.” DHCS 2011.
On the process of embodied play that generates ideas, see also Stephen Ramsay’s book Reading Machines (University of Illinois Press, 2011).

Tags statistics

math methodology statistics undigitized humanities

A brief outburst about numbers.

Post author By tedunderwood
Post date January 3, 2012
10 Comments on A brief outburst about numbers.

In responding to Stanley Fish last week, I tried to acknowledge that the “digital humanities,” in spite of their name, are not centrally about numbers. The movement is very broad, and at the broadest level, it probably has more to do with networked communication than it does with quantitative analysis.

The older tradition of “humanities computing” — which was about numbers — has been absorbed into this larger movement. But it’s definitely the part of DH that humanists are least comfortable with, and it often has to apologize for itself. So, for instance, I’ve spent much of the last year reminding humanists that they’re already using quantitative text mining in the form of search engines — so it can’t be that scary.* Kathleen Fitzpatrick recently wrote a post suggesting that “one key role for a ‘worldly’ digital humanities may well be helping to break contemporary US culture of its unthinking association of numbers with verifiable reality….” Stephen Ramsay’s Reading Machines manages to call for an “algorithmic criticism” while at the same time suggesting that humanists will use numbers in ways that are altogether different from the way scientists use them (or at least different from “scientism,” an admittedly ambiguous term).

I think all three of us (Stephen, Kathleen, and myself) are making strategically necessary moves. Because if you tell humanists that we do (also) need to use numbers the way scientists use them, your colleagues are going to mutter about naïve quests for certainty, shake their heads, and stop listening. So digital humanists are rhetorically required to construct positivist scapegoats who get hypothetically chased from our villages before we can tell people about the exciting new kinds of analysis that are becoming possible. And, to be clear, I think the people I’ve cited (including me) are doing that in fair and responsible ways.

However, I’m in an “eppur si muove” mood this morning, so I’m going to forget strategy for a second and call things the way I see them. <Begin Galilean outburst>

In reality, scientists are not naïve about the relationship between numbers and certainty, because they spend a lot of time thinking about statistics. Statistics is the science of uncertainty, and it insists — as forcefully as any literary theorist could — that every claim comes accompanied by a specific kind of ignorance. Once you accept that, you can stop looking for absolute knowledge, and instead reason concretely about your own relative uncertainty in a given instance. I think humanists’ unfamiliarity with this idea may explain why our critiques of data mining so often taken the form of pointing to a small error buried somewhere in the data: unfamiliarity with statistics forces us to fall back on a black-and-white model of truth, where the introduction of any uncertainty vitiates everything.

Moreover, the branch of statistics most relevant to text mining (Bayesian inference) is amazingly, almost bizarrely willing to incorporate subjective belief into its definition of knowledge. It insists that definitions of probability have to depend not only on observed evidence, but on the “prior probabilities” that we expected before we saw the evidence. If humanists were more familiar with Bayesian statistics, I think it would blow a lot of minds.

I know the line about “lies, damn lies, and so on,” and it’s certainly true that statistics can be abused, as this classic xkcd comic shows. But everything can be abused. The remedy for bad verbal argument is not to “remember that speech should stay in its proper sphere” — it’s to speak better and more critically. Similarly, the remedy for bad quantitative argument is not “remember that numbers have to stay in their proper sphere”; it’s to learn statistics and reason more critically.

Beta_distribution_pdf — possible shapes of the Beta distribution, from Wikpedia

None of this is to say that we can simply borrow tools or methods from scientists unchanged. The humanities have a lot to add — especially when it comes to the social and historical character of human behavior. I think there are fascinating advances taking place in data science right now. But when you take apart the analytic tools that computer scientists have designed, you often find that they’re based on specific mistaken assumptions about the social character of language. For instance, there’s a method called “Topics over Time” that I want to use to identify trends in the written record (Wang and McCallum, 2006). The people who designed it have done really impressive work. But if a humanist takes apart the algorithm underlying this method, they will find that it assumes that every trend can be characterized as a smooth curve called a “Beta distribution.” Whereas in fact, humanists have evidence that the historical trajectory of a topic is often more complex than that, in ways that really matter. So before I can use this tool, I’m going to have to fix that part of the method.

ArmyEnemyMed — The diachronic behavior a topic can actually exhibit.

But this is a problem that can be fixed, in large part, by fixing the numbers. Humanists have a real contribution to make to the science of data mining, but it’s a contribution that can be embodied in specific analytic insights: it’s not just to hover over the field like the ghost of Ben Kenobi and warn it about hubris.

</Galilean outburst>

For related thoughts, somewhat more temperate than the outburst above, see this excellent comment by Matthew Wilkens, responding to a critique of his work by Jeremy Rosen.

* I credit Ben Schmidt for this insight so often that regular readers are probably bored. But for the record: it comes from him.

18c 19c math methodology ngrams

Exploring the relationship between topics and trends.

Post author By tedunderwood
Post date November 18, 2011
1 Comment on Exploring the relationship between topics and trends.

I’ve been talking about correlation since I started this blog. Actually, that was the reason why I did start it: I think literary scholars can get a huge amount of heuristic leverage out of the fact that thematically and socially-related words tend to rise and fall together. It’s a simple observation, and one that stares you in the face as soon as you start to graph word frequencies on the time axis.¹ But it happens to be useful for literary historians, because it tends to uncover topics that also pose periodizable kinds of puzzles. Sometimes the puzzle takes the form of a topic we intuitively recognize (say, the concept of “color”) that increases or decreases in prominence for reasons that remain to be explained:

At other times, the connection between elements of the topic is not immediately intuitive, but the terms are related closely enough that their correlation suggests a pattern worthy of further exploration. The relationship between terms may be broadly historical:

Or it may involve a pattern of expression that characterizes a periodizable style:

Of course, as the semantic relationship between terms becomes less intuitively obvious, scholars are going to wonder whether they’re looking at a real connection or merely an accidental correlation. “Ardent” and “tranquil” seem like opposites; can they really be related as elements of a single discourse? And what’s the relationship to “bosom,” anyway?

Ultimately, questions like this have to be addressed on a case-by-case basis; the significance of the lead has to be fleshed out both with further analysis, and with close reading.

But scholars who are wondering about the heuristic value of correlation may be reassured to know that this sort of lead does generally tend to pan out. Words that correlate with each other across the time axis do in practice tend to appear in the same kinds of volumes. For instance, if you randomly select pairs of words from the top 10,000 words in the Google English ngrams dataset 1700-1849,² measure their correlation with each other in that dataset across the period 1700-1849, and then measure their tendency to appear in the same volumes in a different collection³ (taking the cosine similarity of term vectors in a term-document matrix), the different measures of association correlate with each other strongly. (Pearson’s r is 0.265, significant at p < 0.0005.) Moreover, the relationship holds (less strongly, but still significantly) even in adjacent centuries: words that appear in the same eighteenth-century volumes still tend to rise and fall together in the nineteenth century.

Why should humanists care about the statistical relationship between two measures of association? It means that correlation-mining is in general going to be a useful way of identifying periodizable discourses. If you find a group of words that correlate with each other strongly, and that seem related at first glance, it's probably going to be worthwhile to follow up the hunch. You’re probably looking at a discourse that is bound together both diachronically (in the sense that the terms rise and fall together) and topically (in the sense that they tend to appear in the same kinds of volumes).

Ultimately, literary historians are going to want to assess correlation within different genres; a dataset like Google's, which mixes all genres in a single pool, is not going to be an ideal tool. However, this is also a domain where size matters, and in that respect, at the moment, the ngrams dataset is very helpful. It becomes even more helpful if you correct some of the errors that vitiate it in the period before 1820. A team of researchers at Illinois and Stanford⁴, supported by the Andrew W. Mellon Foundation, has been doing that over the course of the last year, and we're now able to make an early version of the tool available on the web. Right now, this ngram viewer only covers the period 1700-1899, but we hope it will be useful for researchers in that period, because it has mostly corrected the long-s problem that confufes opt1cal charader readers in the 18c — as well as a host of other, less notorious problems. Moreover, it allows researchers to mine correlations in the top 10,000 words of the lexicon, instead of trying words one by one to see whether an interesting pattern emerges. In the near future, we hope to expand the correlation miner to cover the twentieth century as well.

For further discussion of the statistical relationship between topics and trends, see this paper submitted to DHCS 2011.

UPDATE Nov 22, 2011: At DHCS 2011, Travis Brown pointed out to me that Topics Over Time (Wang and McCallum) might mine very similar patterns in a more elegant, generative way. I hope to find a way to test that method, and may perhaps try to build an implementation for it myself.

References
1) Ryan Heuser and I both noticed this pattern last winter. Ryan and Long Le-Khac presented on a related topic at DH2011: Heuser, Ryan, and Le-Khac, Long. “Abstract Values in the 19th Century British Novel: Decline and Transformation of a Semantic Field,” Digital Humanities 2011, Stanford University.

2) Jean-Baptiste Michel*, Yuan Kui Shen, Aviva Presser Aiden, Adrian Veres, Matthew K. Gray, William Brockman, The Google Books Team, Joseph P. Pickett, Dale Hoiberg, Dan Clancy, Peter Norvig, Jon Orwant, Steven Pinker, Martin A. Nowak, and Erez Lieberman Aiden*. “Quantitative Analysis of Culture Using Millions of Digitized Books.” Science (Published online ahead of print: 12/16/2010)

3) The collection of 3134 documents (1700-1849) I used for this calculation was produced by combining ECCO-TCP volumes with nineteenth-century volumes selected and digitized by Jordan Sellers.

4) The SEASR Correlation Analysis and Ngrams Viewer was developed by Loretta Auvil and Boris Capitanu at the Illinois Informatics Institute, modeled on prototypes built by Ted Underwood, University of Illinois, and Ryan Heuser, Stanford.

linguistics math methodology

Identifying diction that characterizes an author or genre: why Dunning’s may not be the best method.

Post author By tedunderwood
Post date November 9, 2011
14 Comments on Identifying diction that characterizes an author or genre: why Dunning’s may not be the best method.

Most of what I’m about to say is directly lifted from articles in corpus linguistics (1, 2), but I don’t think these results have been widely absorbed yet by people working in digital humanities, so I thought it might be worthwhile to share them, while demonstrating their relevance to literary topics.

The basic question is just this: if I want to know what words or phrases characterize an author or genre, how do I find out? As Ben Schmidt has shown in an elegantly visual way, simple mathematical operations won’t work. If you compare ratios (dividing word frequencies in the genre A that interests you by the frequencies in a corpus B used as a point of comparison), you’ll get a list of very rare words. But if you compare the absolute magnitude of the difference between frequencies (subtracting B from A), you’ll get a list of very common words. So the standard algorithm that people use is Dunning’s log likelihood,

— a formula that incorporates both absolute magnitude (O is the observed frequency) and a ratio (O/E is the observed frequency divided by the frequency you would expect). For a more complete account of how this is calculated, see Wordhoard.

But there’s a problem with this measure, as Adam Kilgarriff has pointed out (1, pp. 237-38, 247-48). A word can be common in a corpus because it’s very common in one or two works. For instance, when I characterize early-nineteenth-century poetic diction (1800-1849) by comparing a corpus of 60 volumes of poetry to a corpus of fiction, drama, and nonfiction prose from the same period (3), I get this list:

Much of this looks like “poetic diction” — but “canto” is poetic diction only in a weird sense. It happens to be very common in a few works of poetry that are divided into cantos (works for instance by Lord Byron and Walter Scott). So when everything is added up, yes, it’s more common in poetry — but it doesn’t broadly characterize the corpus. Similar problems occur for a range of other reasons (proper nouns and pronouns can be extremely common in a restricted context).

The solution Kilgarriff offers is to instead use a Mann-Whitney ranks test. This allows us to assess how consistently a given term is more common in one corpus than in another. For instance, suppose I have eight text samples of equal length. Four of them are poetry, and four are prose. I want to know whether “lamb” is significantly more common in the poetry corpus than in prose. A simple form of the Mann-Whitney test would rank these eight samples by the frequency of “lamb” and then add up their respective ranks:

Since most works of poetry “beat” most works of prose in this ranking, the sum of ranks for poetry is higher, in spite of the 31 occurrences of lamb in one work of prose — which is, let us imagine, a novel about sheep-rustling in the Highlands. But a log-likelihood test would have identified this word as more common in prose.

In reality, one never has “equal-sized” documents, but the test is not significantly distorted if one simply replaces absolute frequency with relative frequency (normalized for document size). (If one corpus has on average much smaller documents than the other does, there may admittedly be a slight distortion.) Since the number of documents in each corpus is also going to vary, it’s useful to replace the rank-sum (U) with a statistic ρ (Mann-Whitney rho) that is U, divided by the product of the sizes of the two corpora.

Using this measure of over-representation in a corpus produces a significantly different model of “poetic diction”:

This looks at first glance like a better model. It demotes oddities like “canto,” but also slightly demotes pronouns like “thou” and “his,” which may be very common in some works of poetry but not others. In general, it gives less weight to raw frequency, and more weight to the relative ubiquity of a term in different corpora. Kilgarriff argues that the Mann-Whitney test thereby does a better job of identifying the words that characterize male and female conversation (1, pp. 247-48).

On the other hand, Paul Rayson has argued that by reducing frequency to a rank measure, this approach discards “most of the evidence we have about the distribution of words” (2). For linguists, this poses an interesting, principled dilemma, where two statistically incompatible definitions of “distinctive diction” are pitted against each other. But for a shameless literary hack like myself, it’s no trouble to cut the Gordian knot with an improvised algorithm that combines both measures. For instance, one could multiply rho by the log of Dunning’s log likelihood (represented here as G-squared) …

I don’t yet know how well this algorithm will perform if used for classification or authorship attribution. But it does produce what is for me an entirely convincing portrait of early-nineteenth-century poetic diction:

Of course, once you have an algorithm that convincingly identifies the characteristic diction of a particular genre relative to other publications in the same period, it becomes possible to say how the distinctive diction of a genre is transformed by the passage of time. That’s what I hope to address in my next post.

UPDATE Nov 10, 2011: As I continue to use these tests in different ways (using them e.g. to identify distinctively “fictional” diction, and to compare corpora separated by time) I’m finding the Mann-Whitney ρ measure more and more useful on its own. I think my urge to multiply it by Dunning’s log-likelihood may have been the needless caution of someone who’s using an unfamiliar metric and isn’t sure yet whether it will work unassisted.

References
(1) Adam Kilgarriff, “Comparing Corpora,” International Journal of Corpus Linguistics 6.1 (2001): 97-133.
(2) Paul Rayson, Matrix: A Statistical Method and Software Tool for Linguistic Analysis through Corpus Comparison. Unpublished Ph.D thesis, Lancaster University, 2003, p. 47. Cited in Magali Paquot and Yves Bestgen, “Distinctive words in academic writing: A comparison of three statistical tests for keyword extraction,” Corpora: Pragmatics and Discourse Papers from the 29th International Conference on English Language Research on Computerized Corpora (ICAME 29), Ascona, Switzerland, 14-18 May 2008, p. 254.
(3) The corpora used in this post were selected by Jordan Sellers, mostly from texts available in the Internet Archive, and corrected with a Python script described in this post.

18c LSA math methodology topic modeling

LSA is a marvellous tool, but literary historians may want to customize it for their own discipline.

Post author By tedunderwood
Post date October 16, 2011
9 Comments on LSA is a marvellous tool, but literary historians may want to customize it for their own discipline.

Right now Latent Semantic Analysis is the analytical tool I’m finding most useful. By measuring the strength of association between words or groups of words, LSA allows a literary historian to map themes, discourses, and varieties of diction in a given period.

This approach, more than any other I’ve tried, turns up leads that are useful for me as a literary scholar. But when I talk to other people in digital humanities, I rarely hear enthusiasm for it. Why doesn’t LSA get more love? I see three reasons:

1. The word “semantic” is a false lead: it points away from the part of this technique that would actually interest us. It’s true that Latent Semantic Analysis is based on the observation that a word’s distribution across a collection of documents works remarkably well as a first approximation of its meaning. A program running LSA can identify English synonyms on the TOEFL as well as the average student applying to college from a non-English-speaking country. [1]

But for a literary historian, the value of this technique does not depend on its claim to identify synonyms and antonyms. We may actually be more interested in contingent associations (e.g., “sensibility” — “rousseau” in the list on the left) than we are in the core “meaning” of a word.

I’ll return in a moment to this point. It has important implications, because it means that we want LSA to do something slightly different than linguists and information scientists have designed it to do. The “flaws” they have tried to iron out of the technique may not always be flaws for our purposes.

2. People who do topic-modeling may feel that they should use more-recently-developed Bayesian methods, which are supposed to be superior on theoretical grounds. I’m acknowledging this point just to set it aside; I’ve mused out loud about it once already, and I don’t want to do more musing until I have rigorously compared the two methods. I will say that from the perspective of someone just getting started, LSA is easier to implement than Bayesian topic modeling: it runs faster and scales up more easily.

3. The LSA algorithm provided by an off-the-shelf package is not necessarily the best algorithm for a literary historian. At bottom, that’s why I’m writing this post: humanists who want to use LSA are going to need guidance from people in their own discipline. Computer scientists do acknowledge that LSA requires “tuning, which is viewed as a kind of art.” [2] But they also offer advice about “best practices,” and some of those best practices are defined by disciplinary goals that humanists don’t share.

For instance, the power of LSA is often said to come from “reducing the dimensionality of the matrix.” The matrix in question is a term-document matrix — documents are listed along one side of the matrix, and terms along the other, and each cell of the matrix (tf_i,j) records the number of times term i appears in document j, modified by a weighting algorithm described at the end of this post.

That term-document matrix in and of itself can tell you a lot about the associations between words; all you have to do is measure the similarity between the vectors (columns of numbers) associated with each term. But associations of this kind won’t always reveal synonyms. For instance, “gas” and “petrol” might seem unrelated, because they substitute for each other in different sociolects and are rarely found together. To address that problem, you can condense the matrix by factorizing it with a technique called singular value decomposition (SVD). I’m not going to get into the math here, but the key is that condensing the matrix partially fuses related rows and columns — and as a result, the compressed matrix is able to measure transitive kinds of association. The words “gas” and “petrol” may rarely appear together. But they both appear with the same kinds of other words. So when dimensionality reduction “merges” the rows representing similar documents, “gas” and “petrol” will end up being strongly represented in the same merged rows. A compressed matrix is better at identifying synonyms, and for that reason at information retrieval. So there is a lot of consensus among linguists and information scientists that reducing the number of dimensions in the matrix is a good idea.

But literary historians approach this technique with a different set of goals. We care a lot about differences of sociolect and register, and may even be more interested in those sources of “noise” than we are in purely semantic relations. “Towering,” for instance, is semantically related to “high.” But I could look that up in a dictionary; I don’t need a computer program to tell me that! I might be more interested to discover that “towering” belongs to a particular subset of poetic diction in the eighteenth century. And that is precisely the kind of accident of distribution that dimensionality-reduction is designed to filter out. For that reason, I don’t think literary applications of LSA are always going to profit from the dimensionality-reduction step that other disciplines recommend.

For about eight months now, I’ve been using a version of LSA without dimensionality reduction. It mines associations simply by comparing the cosine-similarity of term vectors in a term-document matrix (weighted in a special way to address differences of document size). But I wanted to get a bit more clarity about the stakes of that choice, so recently I’ve been comparing it to a version of LSA that does use SVD to compress the matrix.

Comparing 18c associations for "delicacy" generated by two different algorithms.

Here’s a quick look at the results. (I’m using 2,193 18c volumes, mostly produced by TCP-ECCO; volumes that run longer than 100,000 words get broken into chunks that can range from 50k-100k words.) In many cases, the differences between LSA with and without compression are not very great. In the case of “delicacy,” for instance, both algorithms indicate that “delicate” has the strongest association. “Politeness” and “tenderness” are also very high on both lists. But compare the second row. The algorithm with compression produces “sensibility” — a close synonym. On the left-hand side, we have “woman.” This is not a synonym for “delicacy,” and if a linguist or computer scientist were evaluating these algorithms, it would probably be rejected as a mistake. But from a literary-historical point of view, it’s no mistake: the association between “delicacy” and femininity is possibly the most interesting fact about the word.

without — The 18c associations of "high" and "towering," in an uncompressed term-document matrix.

In short, compressing the matrix with SVD highlights semantic relationships at the cost of slightly blurring other kinds of association. In the case of “delicacy,” the effect is fairly subtle, but in other cases the difference between the two approaches is substantial. For instance, if you measure the similarity of term vectors in a matrix without compression, “high” and “towering” look entirely different. The main thing you discover about “high” is that it’s used for physical descriptions of landscape (“lies,” “hills”), and the main thing you discover about “towering” is that it’s used in poetic contexts (“flowery,” “glittering”).

The 18c. associations of "high" and "towering," as measured in a term-document matrix that has undergone SVD compression.

In a matrix that has undergone dimensionality reduction with SVD, associations have a much more semantic character, although they are still colored by other dimensions of context. Which of these two algorithms is more useful for humanistic purposes? I think the answer is going to depend on the goals being pursued in a given research project — if you’re interested in “topics” that are strictly semantic, you might want to use an algorithm that reduces dimensionality with SVD. If you’re interested in discourses, sociolects, genres, or types of diction, you might use LSA without dimensionality reduction.

My purpose here isn’t to choose between those approaches; it’s just to remind humanists that the algorithms we borrow from other disciplines are often going to need to be customized for our own disciplinary purposes. Information scientists have designed topic-modeling algorithms that produce semantically unified topics, because semantic categorization is important for them. But in literary history, we also care about other dimensions of language, and we don’t have to judge topic-modeling algorithms by strictly semantic criteria. How should we judge them? It will probably take decades for us to answer that question fully, but the short answer is just — by how well, in practice, they help us locate critically and historically interesting patterns.

A couple of technical notes: A fine point of LSA that can matter a great deal is how you weight the individual cells in the term-document matrix. For the normal LSA algorithm that uses dimensionality reduction, the consensus is that “log-entropy weighting” works well. You take the log of each frequency, and multiply the whole term vector by the entropy of the vector. I have found that this also works well for humanistic purposes.

For LSA without dimensionality reduction, I would recommend weighting cells by subtracting the expected frequency from the observed frequency. This formula “evens the playing field” between common and uncommon words — and it does so, vitally, in a way that gives a word’s absence from a long document more weight than its absence from a short one. (Much of LSA’s power actually comes from learning where a given word tends not to appear. [3]) I have tried various ways of applying log-entropy weighting without compressing the matrix, and I do not recommend it. Those two techniques belong together.

For reasons that remain somewhat mysterious (although the phenomenon itself is widely discussed), dimensionality reduction seems to work best when the number of dimensions retained is in the range of 250-350. Intuitively, it would seem possible to strike a sort of compromise between LSA methods that do and don’t compress the matrix by reducing dimensionality less drastically (perhaps only, say, cutting it by half). But in practice I find that doesn’t work very well; I suspect compression has to reach a certain threshold before the noise inherent in the process starts to cancel itself out and give way to a new sort of order.

[1] Thomas K. Landauer, Peter W. Foltz, and Darrell Latham, An Introduction to Latent Semantic Analysis, Discourse Processes 25 (1998): 259-84. Web reprint, p. 22.
[2] Preslav Nakov, Elena Valchanova, and Galia Angelova, “Towards Deeper Understanding of Latent Sematic Analysis Performance,” Recent Advances in Natural Language Processing, ed. Nicolas Nicolov (Samokov, Bulgaria: John Benjamins, 2004), 299.
[3] Landauer, Foltz, and Latham, p. 24.

18c 19c math ngrams

Words that appear in the same 18c volumes also track each other over time, through the 19c.

Post author By tedunderwood
Post date September 19, 2011
No Comments on Words that appear in the same 18c volumes also track each other over time, through the 19c.

I wrote a long post last Friday arguing that topic-modeling an 18c collection is a reliable way of discovering eighteenth- and nineteenth-century trends, even in a different collection.

But when I woke up on Saturday I realized that this result probably didn’t depend on anything special about “topic modeling.” After all, the topic-modeling process I was using was merely a form of clustering. And all the clustering process does is locate the hypothetical centers of more-or-less-evenly-sized clouds of words in vector space. It seemed likely that the specific locations of these centers didn’t matter. The key was the underlying measure of association between words — “cosine similarity in vector space,” which is a fancy way of saying “tendency to be common in the same 18c volumes.” Any group of words that were common (and uncommon) in the same 18c volumes would probably tend to track each other over time, even into the next century.

GratifyCurves540 — Six words that tend to occur in the same 18c volumes as 'gratify' (in TCP-ECCO), plotted over time in a different collection (a corrected version of Google ngrams).

To test this I wrote a script that chose 200 words at random from the top 5000 in a collection of 2,193 18c volumes (drawn from TCP-ECCO with help from Laura Mandell), and then created a cluster around each word by choosing the 25 words most likely to appear in the same volumes (cosine similarity). Would pairs of words drawn from these randomly distributed clusters also show a tendency to correlate with each other over time?

They absolutely do. The Fisher weighted mean pairwise r for all possible pairs drawn from the same cluster is .267 in the 18c and .284 in the 19c (the 19c results are probably better because Google’s dataset is better in the 19c even after my efforts to clean the 18c up*). At n = 100 (measured over a century), both correlations have rock-solid statistical significance, p < .01. And in case you're wondering … yes, I wrote another script to test randomly selected words using the same statistical procedure, and the mean pairwise r for randomly selected pairs (factoring out, as usual, partial correlation with the larger 5000-word group they’re selected from) is .0008. So I feel confident that the error level here is low.**

What does this mean, concretely? It means that the universe of word-frequency data is not chaotic. Words that appear in the same discursive contexts tend, strongly, to track each other over time, and (although I haven’t tested this rigorously yet), it’s not hard to see that the converse proposition is also going to hold true: words that track each other over time are going to tend to have contextual associations as well.

To put it even more bluntly: pick a word, any word! We are likely to be able to define not just a topic associated with that word, but a discourse — a group of words that are contextually related and that also tend to wax and wane together over time. I don’t imagine that in doing so we prove anything of humanistic significance, but I do think it means that we can raise several thousand significant questions. To start with: what was the deal with eagerness, gratification, and disappointment in the second half of the eighteenth century?

* A better version of Google’s 18c dataset may be forthcoming from the NCSA.

** For people who care about the statistical reliability of data-mining, here’s the real kicker: if you run a Benjamini-Hochberg procedure on these 200 randomly-generated clusters, 134 of them have significance at p < .05 in the 19c even after controlling for the false discovery rate. To put that more intelligibly, these are guaranteed not to be xkcd’s green jelly beans. The coherence of these clusters is even greater than the ones produced by topic-modeling, but that’s probably because they are on average slightly smaller (25 words); I have yet to test the relative importance of different generation procedures while holding cluster size rigorously constant.

18c 19c math methodology topic modeling trend mining

Topics tend to be trends. Really: p < .05!

Post author By tedunderwood
Post date September 16, 2011
No Comments on Topics tend to be trends. Really: p < .05!

While I’m fascinated by cases where the frequencies of two, or ten, or twenty words closely parallel each other, my conscience has also been haunted by a problem with trend-mining — which is that it always works. There are so many words in the English language that you’re guaranteed to find groups of them that correlate, just as you’re guaranteed to find constellations in the night sky. Statisticians call this the problem of “multiple comparisons”; it rests on a fallacy that’s nicely elucidated in this classic xkcd comic about jelly beans.

Simply put: it feels great to find two conceptually related words that correlate over time. But we don’t know whether this is a significant find, unless we also know how many potentially related words don’t correlate.

One way to address this problem is to separate the process of forming hypotheses from the process of testing them. For instance, we could use topic modeling to divide the lexicon up into groups of terms that occur in the same contexts, and then predict that those terms will also correlate with each other over time. In making that prediction, we turn an undefined universe of possible comparisons into a finite set.

Once you create a set of topics, plotting their frequencies is simple enough. But plotting the aggregate frequency of a group of words isn’t the same thing as “discovering a trend,” unless the individual words in the group actually correlate with each other over time. And it’s not self-evident that they will.

Silence2 — The top 15 words in topic #91, "Silence/Listened," and their cosine similarity to the centroid.

So I decided to test the hypothesis that they would. I used semi-fuzzy clustering to divide one 18c collection (TCP-ECCO) into 200 groups of words that tend to appear in the same volumes, and then tested the coherence of those topics over time in a different 18c collection (a much-cleaned-up version of the Google ngrams dataset I produced in collaboration with Loretta Auvil and Boris Capitanu at the NCSA). Testing hypotheses in a different dataset than the one that generated them is a way of ensuring that we aren’t simply rediscovering the same statistical accidents a second time.

To make a long story short, it turns out that topics have a statistically significant tendency to be trends (at least when you’re working with a century-sized domain). Pairs of words selected from the same topic correlated significantly with each other even after factoring out other sources of correlation*; the Fisher weighted mean r for all possible pairs was 0.223, which measured over a century (n = 100) is significant at p < .05.

In practice, the coherence of different topics varied widely. And of course, any time you test a bunch of hypotheses in a row you're going to get some false positives. So the better way to assess significance is to control for the "false discovery rate." When I did that (using the Benjamini-Hochberg method) I found that 77 out of the 200 topics cohered significantly as trends.

There are a lot of technical details, but I'll defer them to a footnote at the end of this post. What I want to emphasize first is the practical significance of the result for two different kinds of researchers. If you're interested in mining diachronic trends, then it may be useful to know that topic-modeling is a reliable way of discovering trends that have real statistical significance and aren’t just xkcd’s “green jelly beans.”

The top 15 terms in topic #89, "Enemy/Attacked," and their cosine similarity to the centroid.

Conversely, if you're interested in topic modeling, it may be useful to know that the topics you generate will often be bound together by correlation over time as well. (In fact, as I’ll suggest in a moment, topics are likely to cohere as trends beyond the temporal boundaries of your collection!)

Finally, I think this result may help explain a phenomenon that Ryan Heuser, Long Le-Khac, and I have all independently noticed: which is that groups of words that correlate over time in a given collection also tend to be semantically related. I've shown above that topic modeling tends to produce diachronically coherent trends. I suspect that the converse proposition is also true: clusters of words linked by correlation over time will turn out to have a statistically significant tendency to appear in the same contexts.

Why are topics and trends so closely related? Well, of course, when you’re topic-modeling a century-long collection, co-occurrence has a diachronic dimension to start with. So the boundaries between topics may already be shaped by change over time. It would be interesting to factor time out of the topic-modeling process, in order to see whether rigorously synchronic topics would still generate diachronic trends.

I haven’t tested that yet, but I have tried another kind of test, to rule out the possibility that we’re simply rediscovering the same trends that generated the topics in the first place. Since the Google dataset is very large, you can also test whether 18c topics continue to cohere as trends in the nineteenth century. As it turns out, they do — and in fact, they cohere slightly more strongly! (In the 19c, 88 out of 200 18c topics cohered significantly as trends.) The improvement is probably a clue that Google’s dataset gets better in the nineteenth century (which god knows, it does) — but even if that’s true, the 19c result would be significant enough on its own to show that topic modeling has considerable predictive power.

Practically, it’s also important to remember that “trends” can play out on a whole range of different temporal scales.

For instance, here’s the trend curve for topic #91, “Silence / Listened,” which is linked to the literature of suspense, and increases rather gradually and steadily from 1700 to the middle of the nineteenth century.

By contrast, here’s the trend curve for topic #89, “Enemy/Attacked,” which is largely used in describing warfare. It doesn’t change frequency markedly from beginning to end; instead it bounces around from decade to decade with a lot of wild outliers. But it is in practice a very tightly-knit trend: a pair of words selected from this topic will have on average 31% of their variance in common. The peaks and outliers are not random noise: they’re echoes of specific armed conflicts.

* Technical details: Instead of using Latent Dirichlet Allocation for topic modeling, I used semi-fuzzy c-means clustering on term vectors, where term vectors are defined in the way I describe in this technical note. I know LDA is the standard technique, and it seems possible that it would perform even better than my clustering algorithm does. But in a sufficiently large collection of documents, I find that a clustering algorithm produces, in practice, very coherent topics, and it has some other advantages that appeal to me. The “semi-fuzzy” character of the algorithm allows terms to belong to more than one cluster, and I use cosine similarity to the centroid to define each term’s “degree of membership” in a topic.

I only topic-modeled the top 5000 words in the TCP-ECCO collection. So in measuring pairwise correlations of terms drawn from the same topic, I had to calculate it as a partial correlation, controlling for the fact that terms drawn from the top 5k of the lexicon are all going to have, on average, a slight correlation with each other simply by virtue of being drawn from that larger group.