I should say up front that this is going to be a geeky post about things that happen under the hood of the car. Many readers may be better served by scrolling down to “Trends, topics, and trending topics,” which has more to say about the visible applications of text mining.
I’ve developed a clustering methodology that I like pretty well. It allows me to map patterns of usage in a large collection by treating each term as a vector; I assess how often words occur together by measuring the angle between vectors, and then group the words with Ward’s clustering method. This produces a topic tree that seems to be both legible (in the sense that most branches have obvious affinities to a genre or subject category) and surprising (in the sense that they also reveal thematic connections I wouldn’t have expected). It’s a relatively simple technique that does what I want to do, practically, as a literary historian. (You can explore this map of eighteenth-century diction to check it out yourself; and I should link once again to Sapping Attention, which convinced me clustering could be useful.)
But as I learn more about Bayesian statistics, I’m coming to realize that it’s debatable whether the clusters of terms I’m finding count as topics at all. The topic-modeling algorithms that have achieved wide acceptance (for instance, Latent Dirichlet Allocation) are based on a clear definition of what a “topic” is. They hypothesize that the observed complexity of usage patterns is actually produced by a smaller set of hidden variables. Because those variables can be represented as lists of words, they’re called topics. But the algorithm isn’t looking for thematic connections between words so much as resolving a collection into a set of components or factors that could have generated it. In this sense, it’s related to a technique like Principal Component Analysis.
Deriving those hidden variables is a mathematical task of considerable complexity. In fact, it’s impossible to derive them precisely: you have to estimate. I can only understand the math for this when my head is constantly bathed in cool running water to keep the processor from overheating, so I won’t say much more about it — except that “factoring” is just a metaphor I’m using to convey the sort of causal logic involved. The actual math involves Bayesian inference rather than algebra. But it should be clear, anyway, that this is completely different from what I’m doing. My approach isn’t based on any generative model, and can’t claim to reveal the hidden factors that produce texts. It simply clusters words that are in practice associated with each other in a corpus.
I haven’t tried the Bayesian approach yet, but it has some clear advantages. For one thing, it should work better for purposes of classification and information retrieval, because it’s looking for topics that vary (at least in principle) independently of each other.* If you want to use the presence of a topic in a document to guide classification, this matters. A topic that correlated positively or negatively with another topic would become redundant; it wouldn’t tell you much you didn’t already know. It makes sense to me that people working in library science and information retrieval have embraced an approach that resolves a collection into independent variables, because problems of document classification are central to those disciplines.
On the other hand, if you’re interested in mapping associations between terms, or topics, the clustering approach has advantages. It doesn’t assume that topics vary independently. On the contrary, it’s based on a measure of association between terms that naturally extends to become a measure of association between the topics themselves. The clustering algorithm produces a branching tree structure that highlights some of the strongest relationships and contrasts, but you don’t have to stop there: any list of terms can be treated as a vector, and compared to any other list of terms.

Moreover, this flexibility means that you don’t have to treat the boundaries of “topics” as fixed. For instance, here’s part of the eighteenth-century tree that I found interesting: the words on this branch seemed to imply a strange connection between temporality and feeling, and they turned out to be particularly common in late-eighteenth-century novels by female writers. Intriguing, but we’re just looking at five words. Maybe the apparent connection is a coincidence. Besides, “cried” is ambiguous; it can mean “exclaimed” in this period more often than it means “wept.” How do we know what to make of a clue like this? Well, given the nature of the vector space model that produced the tree, you can do this: treat the cluster of terms itself as a vector, and look for other terms that are strongly related to it. When I did that, I got a list that confirmed the apparent thematic connection, and helped me begin to understand it.

This is, very definitely, a list of words associated with temporality (moment, hastily, longer, instantly, recollected) and feeling (felt, regret, anxiety, astonishment, agony). Moreover, it’s fairly clear that the common principle uniting them is something like “suspense” (waiting, eagerly, impatiently, shocked, surprise). Gender is also involved — which might not have been immediately evident from the initial cluster, because gendered words were drawn even more strongly to other parts of the tree. But the associational logic of the clustering process makes it easy to treat topic boundaries as porous; the clusters that result don’t have to be treated as rigid partitions; they’re more appropriately understood as starting-places for exploration of a larger associational web.
[This would incidentally be my way of answering a valid critique of clustering — that it doesn’t handle polysemy well. The clustering algorithm has to make a choice when it encounters a word like “cried.” The word might in practice have different sets of associations, based on different uses (weep/exclaim), but it’s got to go in one branch or another. It can’t occupy multiple locations in the tree. We could try to patch that problem, but I think it may be better to realize that the problem isn’t as important as it appears, because the clusters aren’t end-points. Whether a term is obviously polysemous, or more subtly so, we’re always going to need to make a second pass where we explore the associations of the cluster itself in order to shake off the artificiality of the tree structure, and get a richer sense of multi-dimensional context. When we do that we’ll pick up words like “herself,” which could justifiably be located at any number of places in the tree.]
Much of this may already be clear to people in informatics, but I had to look at the math in order to understand that different kinds of “topic modeling” are really doing different things. Humanists are going to have some tricky choices to make here that I’m not sure we understand yet. Right now the Bayesian “factoring” approach is more prominent, partly because the people who develop text-mining algorithms tend to work in disciplines where classification problems are paramount, and where it’s important to prove that they can be solved without human supervision. For literary critics and historians, the appropriate choice is less clear. We may sometimes be interested in classifying documents (for instance, when we’re reasoning about genre), and in that case we too may need something like Latent Dirichlet Allocation or Principal Component Analysis to factor out underlying generative variables. But we’re just as often interested in thematic questions — and I think it’s possible that those questions may be more intuitively, and transparently, explored through associational clustering. To my mind, it’s fair to call both processes “topic modeling” — but they’re exploring topics of basically different kinds.
Postscript: I should acknowledge that there are lots of ways of combining these approaches, either by refining LDA itself, or by combining that sort of topic-factoring approach with an associational web. My point isn’t that we have to make a final choice between these processes; I’m just reflecting that, in principle, they do different things.
* (My limited understanding of the math behind Latent Dirichlet Allocation is based on a 2009 paper by D.M. Blei and J. D. Lafferty available here.)
Month: April 2011
I’ve developed a text-mining strategy that identifies what I call “trending topics” — with apologies to Twitter, where the term is used a little differently. These are diachronic patterns that I find practically useful as a literary historian, although they don’t fit very neatly into existing text-mining categories.
A “topic,” as the term is used in text-mining, is a group of words that occur together in a way that defines a thematic focus. Cameron Blevin’s analysis of Martha Ballard’s diary is often cited as an example: Blevin identifies groups of words that seem to be associated, for instance, with “midwifery,” “death,” or “gardening,” and tracks these topics over the course of the diary.
“Trends” haven’t received as much attention as topics, but we need some way to describe the pattern that Google’s ngram viewer has made so visible, where groups of related words rise and fall together across long periods of time. I suspect “trend” is as a good a name for this phenomenon as we’ll get.
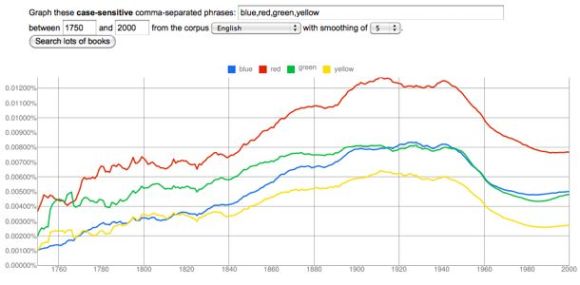
From 1750 to 1920, the prominence of color vocabulary increases by a factor of three, for instance: and when it does, the names of different colors track each other very closely. I would call this a trend. Moreover, it’s possible to extend the principle that conceptually related words rise and fall together beyond cases like the colors and seasons where we’re dealing with an obvious physical category.
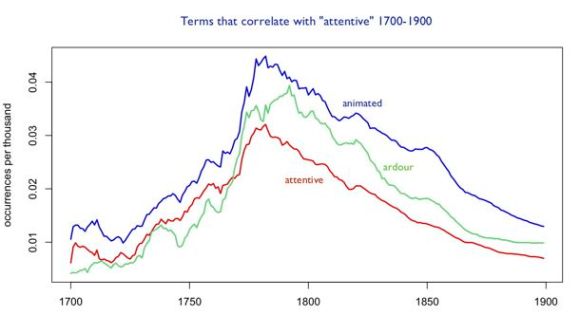
“Animated,” “attentive,” and “ardour” track each other almost as closely as the names of primary colors (the correlation coefficients are around 0.8), and they characterize conduct in ways that are similar enough to suggest that we’re looking at the waxing and waning not just of a few random words, but of a conceptual category — say, a particular sort of interest in states of heightened receptiveness or expressivity.
I think we could learn a lot by thoughtfully considering “trends” of this sort, but it’s also a kind of evidence that’s not easy to interpret, and that could easily be abused. A lot of other words correlate almost as closely with “attentive,” including “propriety,” “elegance,” “sentiments,” “manners,” “flattering,” and “conduct.” Now, I don’t think that’s exactly a random list (these terms could all be characterized loosely as a discourse of manners), but it does cover more conceptual ground than I initially indicated by focusing on words like “animated” and “ardour.” And how do we know that any of these terms actually belonged to the same “discourse”? Perhaps the books that talked about “conduct” were careful not to talk about “ardour”! Isn’t it possible that we have several distinct discourses here that just happened to be rising and falling at the same time?
In order to answer these questions, I’ve been developing a technique that mines “trends” that are at the same time “topics.” In other words, I look for groups of terms that hold together both in the sense that they rise and fall together (correlation across time), and in the sense that they tend to be common in the same documents (co-occurrence). My way of achieving this right now is a two-stage process: first I mine loosely defined trends from the Google ngrams dataset (long lists of, say, one hundred closely correlated words), and then I send those trends to a smaller, generically diverse collection (including everything from sermons to plays) where I can break the list into clusters of terms that tend to occur in the same kinds of documents.
I do this with the same vector space model and hierarchical clustering technique I’ve been using to map eighteenth-century diction on a larger scale. It turns the list of correlated words into a large, branching tree. When you look at a single branch of that tree you’re looking at what I would call a “trending topic” — a topic that represents, not a stable, more-or-less-familiar conceptual category, but a dynamically-linked set of concepts that became prominent at the same time, and in connection with each other.

Here, for instance, is a branch of a larger tree that I produced by clustering words that correlate with “manners” in the eighteenth century. It may not immediately look thematically coherent. We might have expected “manners” to be associated with words like “propriety” or “conduct” (which do in fact correlate with it over time), but when we look at terms that change in correlated ways and occur in the same volumes, we get a list of words that are largely about wealth and rank (“luxury,” “opulence,” “magnificence”), as well as the puzzling “enervated.” To understand a phenomenon like this, you can simply reverse the process that generated it, by using the list as a search query in the eighteenth-century collection it’s based on. What turned up in this case were, pre-eminently, a set of mid-eighteenth-century works debating whether modern commercial opulence, and refinements in the arts, have had an enervating effect on British manners and civic virtue. Typical examples are John Brown’s Estimate of the Manners and Principles of the Times (1757) and John Trusler’s Luxury no Political Evil but Demonstratively Proved to be Necessary to the Preservation and Prosperity of States (1781). I was dimly aware of this debate, but didn’t grasp how central it became to debate about manners, and certainly wasn’t familiar with the works by Brown and Trusler.
I feel like this technique is doing what I want it to do, practically, as a literary historian. It makes the ngram viewer something more than a provocative curiosity. If I see an interesting peak in a particular word, I can can map the broader trend of which it’s a part, and then break that trend up into intersecting discourses, or individual works and authors.
Admittedly, there’s something inelegant about the two-stage process I’m using, where I first generate a list of terms and then use a smaller collection to break the list into clusters. When I discussed the process with Ben Schmidt and Miles Efron, they both, independently, suggested that there ought to be some simpler way of distinguishing “trends” from “topics” in a single collection, perhaps by using Principal Component Analysis. I agree about that, and PCA is an intriguing suggestion. On the other hand, the two-stage process is adapted to the two kinds of collections I actually have available at the moment: on the one hand, the Google dataset, which is very large and very good at mapping trends with precision, but devoid of metadata, on the other hand smaller, richer collections that are good at modeling topics, but not large enough to produce smooth trend lines. I’m going to experiment with Principal Component Analysis and see what it can do for me, but in the meantime — speaking as a literary historian rather than a computational linguist — I’m pretty happy with this rough-and-ready way of identifying trending topics. It’s not an analytical tool: it’s just a souped-up search technology that mines trends and identifies groups of works that could help me understand them. But as a humanist, that’s exactly what I want text mining to provide.
The key to all mythologies.
Well, not really. But it is a classifying scheme that might turn out to be as loopy as Casaubon’s incomplete project in Middlemarch, and I thought I might embrace the comparison to make clear that I welcome skepticism.

In reality, it’s just a map of eighteenth-century diction. I took the 1,650 most common words in eighteenth-century writing, and asked my iMac to group them into clusters that tend to be common in the same eighteenth-century works. Since the clustering program works recursively, you end up with a gigantic branching tree that reveals how closely words are related to each other in 18c practice. If they appear on the same “branch”; they tend to occur in the same works. If they appear on the same “twig,” that tendency is even stronger.
You wouldn’t necessarily think that two words happening to occur in the same book would tell you much, but when you’re dealing with a large number of documents, it seems there’s a lot of information contained in the differences between them. In any case, this technique produced a detailed map of eighteenth-century topics that seemed — to me, anyway — surprisingly illuminating. To explore a couple of branches, or just marvel at this monument of digital folly, click here, or on the illustration to the right. That’ll take you through to a page where you can click on whichever branches interest you. (Click on the links in the right-hand margin, not the annotations on the tree itself.) To start with, I recommend Branch 18, which is a sort of travel narrative, Branch 13, which is 18c poetic diction in a nutshell, and Branch 5, which is saying something about gender and/or sexuality that I don’t yet understand.
If you want to know exactly how this was produced, and contrast it to other kinds of topic modeling, I describe the technique in this “technical note.” I should also give thanks to the usual cast of characters. Ryan Heuser and Ben Schmidt have produced analogous structures which gave me the idea of attempting this. Laura Mandell and 18th Connect helped me obtain the eighteenth-century texts on which the tree was based.
[UPDATE April 7: The illustrations in this post are now out of date, though some of the explanation may still be useful. The kinds of diction mapped in these illustrations are now mapped better in branches 13-14, 18, and 1 of this larger topic tree.] While trying to understand the question I posed in my last post (why did style become less “conversational” in the 18th century?), I stumbled on a technique that might be useful to other digital humanists. I thought I might pause to describe it.
The technique is basically a kind of topic modeling. But whereas most topic modeling aims to map recurring themes in a single work, this technique maps topics at the corpus level. In other words, it identifies groups of words that are linked by the fact that they tend to occur in the same kinds of books. I’m borrowing this basic idea from Ben Schmidt, who used tf-idf scores to do something similar. I’ve taken a slightly different approach by using a “vector space model,” which I prefer for reasons I’ll describe in some technical notes. But since you’ll need to see results before you care about the how, let me start by showing you what the technique produces.

This branch of a larger tree structure was produced by a clustering program that groups words together when they resemble each other according to some measure of similarity. In this case I defined “similarity” as a tendency to occur in the same eighteenth-century texts. Since the tree structure records the sequence of grouping operations, it can register different nested levels of similarity. In the image above, for instance, we can see that “proud” and “pride” are more likely to occur in the same texts than either is to occur together with “smile” or “gay.” But since this is just one branch of a much larger tree, all of these words are actually rather likely to occur together.
This tree is based on a generically diverse collection of 18c texts drawn from ECCO-TCP with help from 18thConnect, and was produced by applying the clustering program I wrote to the 1350 most common words in that collection. The branch shown above represents about 1/50th of the whole tree. But I’ve chosen this branch to start with because it neatly illustrates the underlying principle of association. What do these words have in common? They’re grouped together because they appear in the same kinds of texts, and it’s fairly clear that the “kinds” in this case are poetic. We could sharpen that hypothesis by using this list of words as a search query to see exactly which texts it turns up, but given the prevalence of syncope (“o’er” and “heav’n”), poetry is a safe guess.
It is true that semantically related words tend to be strongly grouped in the tree. Ease/care, charms/fair and so on, are closely linked. But that isn’t a rule built into the algorithm I’m using; the fact that it happens is telling us something about the way words are in practice distributed in the collection. As a result, you get a snapshot of eighteenth century “poetic diction,” not just in the sense of specialized words like “oft,” but in the sense that you can see which themes counted as “poetic” in the eighteenth century, and possibly gather some clues about the way those themes were divided into groups. (In order to find out whether those divisions were generic or historical, you would need to turn the process around and use the sublists as search queries.)
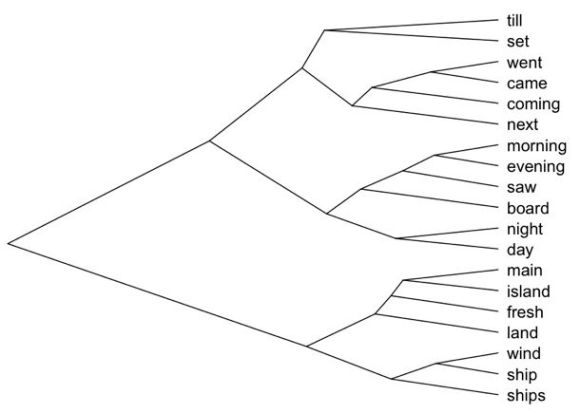
Here’s another part of the tree, showing words that are grouped together because they tend to appear in accounts of travel. The words at the bottom of the image (from “main” to “ships”) are very clearly connected to maritime travel, and the verbs of motion at the top of the image are connected to travel more generally. It’s less obvious that diurnal rhythms like morning/evening and day/night would be described heavily in the same contexts, but apparently they are.
In trees like these, some branches are transparently related to a single genre or subject category, while others are semantically fascinating but difficult to interpret as reflections of a single genre. They may well be produced by the intersection or overlap of several different generic (or historical) categories, and it’ll require more work to understand the nature of the overlap. In a few days I’ll post an overview of the architecture of the whole 1350-word eighteenth-century tree. It’ll be interesting to see how its architecture changes when I slide the collection forward in time to cover progressively later periods (like, say, 1750-1850). But I’m finding the tree interesting for reasons that aren’t limited to big architectural questions of classification: there are interesting thematic clues at every level of the structure. Here’s a portion of one that I constructed with a slightly different list of words.

Broadly, I would say that this is the language of sentiment: “alarm,” “softened,” “shocked,” “warmest,” “unfeeling.” But there are also ringers in there, and in a way they’re the most interesting parts. For instance, why are “moment” and “instantly” part of the language of sentiment in the eighteenth century?
