trend mining – The Stone and the Shell

Topics tend to be trends. Really: p < .05!

While I’m fascinated by cases where the frequencies of two, or ten, or twenty words closely parallel each other, my conscience has also been haunted by a problem with trend-mining — which is that it always works. There are so many words in the English language that you’re guaranteed to find groups of them that correlate, just as you’re guaranteed to find constellations in the night sky. Statisticians call this the problem of “multiple comparisons”; it rests on a fallacy that’s nicely elucidated in this classic xkcd comic about jelly beans.

Simply put: it feels great to find two conceptually related words that correlate over time. But we don’t know whether this is a significant find, unless we also know how many potentially related words don’t correlate.

One way to address this problem is to separate the process of forming hypotheses from the process of testing them. For instance, we could use topic modeling to divide the lexicon up into groups of terms that occur in the same contexts, and then predict that those terms will also correlate with each other over time. In making that prediction, we turn an undefined universe of possible comparisons into a finite set.

Once you create a set of topics, plotting their frequencies is simple enough. But plotting the aggregate frequency of a group of words isn’t the same thing as “discovering a trend,” unless the individual words in the group actually correlate with each other over time. And it’s not self-evident that they will.

Silence2 — The top 15 words in topic #91, "Silence/Listened," and their cosine similarity to the centroid.

So I decided to test the hypothesis that they would. I used semi-fuzzy clustering to divide one 18c collection (TCP-ECCO) into 200 groups of words that tend to appear in the same volumes, and then tested the coherence of those topics over time in a different 18c collection (a much-cleaned-up version of the Google ngrams dataset I produced in collaboration with Loretta Auvil and Boris Capitanu at the NCSA). Testing hypotheses in a different dataset than the one that generated them is a way of ensuring that we aren’t simply rediscovering the same statistical accidents a second time.

To make a long story short, it turns out that topics have a statistically significant tendency to be trends (at least when you’re working with a century-sized domain). Pairs of words selected from the same topic correlated significantly with each other even after factoring out other sources of correlation*; the Fisher weighted mean r for all possible pairs was 0.223, which measured over a century (n = 100) is significant at p < .05.

In practice, the coherence of different topics varied widely. And of course, any time you test a bunch of hypotheses in a row you're going to get some false positives. So the better way to assess significance is to control for the "false discovery rate." When I did that (using the Benjamini-Hochberg method) I found that 77 out of the 200 topics cohered significantly as trends.

There are a lot of technical details, but I'll defer them to a footnote at the end of this post. What I want to emphasize first is the practical significance of the result for two different kinds of researchers. If you're interested in mining diachronic trends, then it may be useful to know that topic-modeling is a reliable way of discovering trends that have real statistical significance and aren’t just xkcd’s “green jelly beans.”

The top 15 terms in topic #89, "Enemy/Attacked," and their cosine similarity to the centroid.

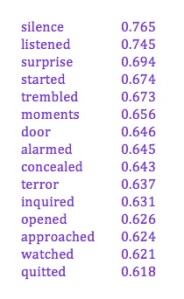
Conversely, if you're interested in topic modeling, it may be useful to know that the topics you generate will often be bound together by correlation over time as well. (In fact, as I’ll suggest in a moment, topics are likely to cohere as trends beyond the temporal boundaries of your collection!)

Finally, I think this result may help explain a phenomenon that Ryan Heuser, Long Le-Khac, and I have all independently noticed: which is that groups of words that correlate over time in a given collection also tend to be semantically related. I've shown above that topic modeling tends to produce diachronically coherent trends. I suspect that the converse proposition is also true: clusters of words linked by correlation over time will turn out to have a statistically significant tendency to appear in the same contexts.

Why are topics and trends so closely related? Well, of course, when you’re topic-modeling a century-long collection, co-occurrence has a diachronic dimension to start with. So the boundaries between topics may already be shaped by change over time. It would be interesting to factor time out of the topic-modeling process, in order to see whether rigorously synchronic topics would still generate diachronic trends.

I haven’t tested that yet, but I have tried another kind of test, to rule out the possibility that we’re simply rediscovering the same trends that generated the topics in the first place. Since the Google dataset is very large, you can also test whether 18c topics continue to cohere as trends in the nineteenth century. As it turns out, they do — and in fact, they cohere slightly more strongly! (In the 19c, 88 out of 200 18c topics cohered significantly as trends.) The improvement is probably a clue that Google’s dataset gets better in the nineteenth century (which god knows, it does) — but even if that’s true, the 19c result would be significant enough on its own to show that topic modeling has considerable predictive power.

Practically, it’s also important to remember that “trends” can play out on a whole range of different temporal scales.

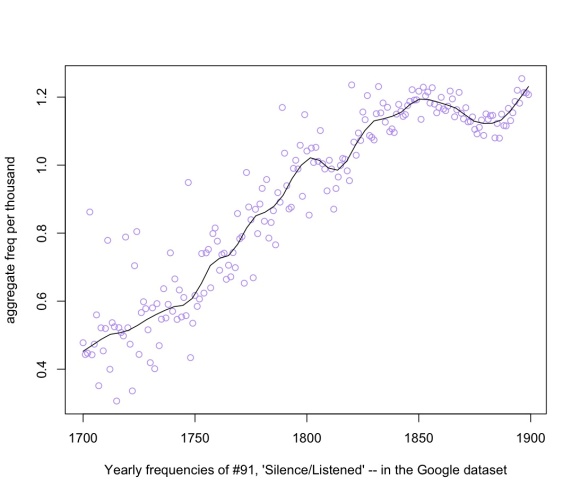
For instance, here’s the trend curve for topic #91, “Silence / Listened,” which is linked to the literature of suspense, and increases rather gradually and steadily from 1700 to the middle of the nineteenth century.

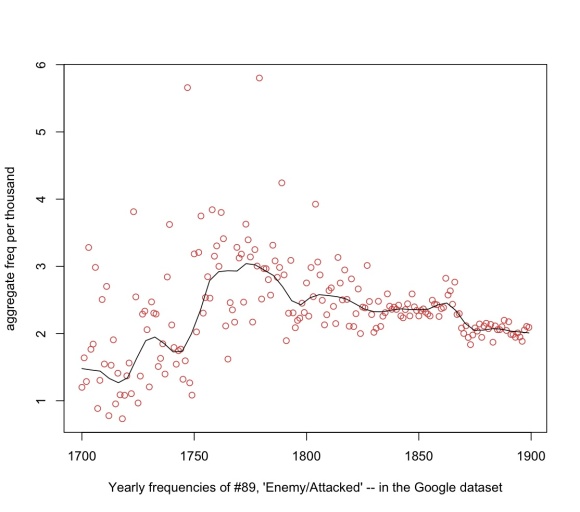
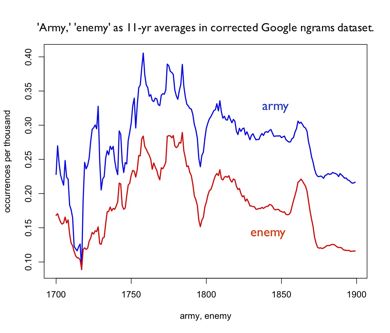
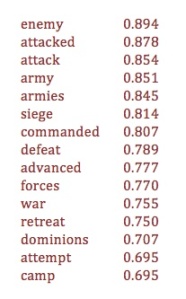
By contrast, here’s the trend curve for topic #89, “Enemy/Attacked,” which is largely used in describing warfare. It doesn’t change frequency markedly from beginning to end; instead it bounces around from decade to decade with a lot of wild outliers. But it is in practice a very tightly-knit trend: a pair of words selected from this topic will have on average 31% of their variance in common. The peaks and outliers are not random noise: they’re echoes of specific armed conflicts.

* Technical details: Instead of using Latent Dirichlet Allocation for topic modeling, I used semi-fuzzy c-means clustering on term vectors, where term vectors are defined in the way I describe in this technical note. I know LDA is the standard technique, and it seems possible that it would perform even better than my clustering algorithm does. But in a sufficiently large collection of documents, I find that a clustering algorithm produces, in practice, very coherent topics, and it has some other advantages that appeal to me. The “semi-fuzzy” character of the algorithm allows terms to belong to more than one cluster, and I use cosine similarity to the centroid to define each term’s “degree of membership” in a topic.

I only topic-modeled the top 5000 words in the TCP-ECCO collection. So in measuring pairwise correlations of terms drawn from the same topic, I had to calculate it as a partial correlation, controlling for the fact that terms drawn from the top 5k of the lexicon are all going to have, on average, a slight correlation with each other simply by virtue of being drawn from that larger group.

Identifying topics with a specific kind of historical timeliness.

Benjamin Schmidt has been posting some fascinating reflections on different ways of analyzing texts digitally and characterizing the affinities between them.

I’m tempted to briefly comment on a technique of his that I find very promising. This is something that I don’t yet have the tools to put into practice myself, and perhaps I shouldn’t comment until I do. But I’m just finding the technique too intriguing to resist speculating about what might be done with it.

Basically, Schmidt describes a way of mapping the relationships between terms in a particular archive. He starts with a word like “evolution,” identifies texts in his archive that use the word, and then uses tf-idf weighting to identify the other words that, statistically, do most to characterize those texts.

After iterating this process a few times, he has a list of something like 100 terms that are related to “evolution” in the sense that this whole group of terms tends, not just to occur in the same kinds of books, but to be statistically prominent in them. He then uses a range of different clustering algorithms to break this list into subsets. There is, for instance, one group of terms that’s clearly related to social applications of evolution, another that seems to be drawn from anatomy, and so on. Schmidt characterizes this as a process that maps different “discourses.” I’m particularly interested in his decision not to attempt topic modeling in the strict sense, because it echoes my own hesitation about that technique:

In the language of text analysis, of course, I’m drifting towards not discourses, but a simple form of topic modeling. But I’m trying to only submerge myself slowly into that pool, because I don’t know how well fully machine-categorized topics will help researchers who already know their fields. Generally, we’re interested in heavily supervised models on locally chosen groups of texts.

This makes a lot of sense to me. I’m not sure that I would want a tool that performed pure “topic modeling” from the ground up — because in a sense, the better that tool performed, the more it might replicate the implicit processing and clustering of a human reader, and I already have one of those.

Schmidt’s technique is interesting to me because the initial seed word gives it what you might call a bias, as well as a focus. The clusters he produces aren’t necessarily the same clusters that would emerge if you tried to map the latent topics of his whole archive from the ground up. Instead, he’s producing a map of the semantic space surrounding “evolution,” as seen from the perspective of that term. He offers this less as a finished product than as an example of a heuristic that humanists might use for any keyword that interested them, much in the way we’re now accustomed to using simple search strategies. Presumably it would also be possible to move from the semantic clusters he generates to a list of the documents they characterize.

I think this is a great idea, and I would add only that it could be adapted for a number of other purposes. Instead of starting with a particular seed word, you might start with a list of terms that happen to be prominent in a particular period or genre, and then use Schmidt’s technique of clustering based on tf-idf correlations to analyze the list. “Prominence” can be defined in a lot of different ways, but I’m particularly interested in words that display a similar profile of change across time.

For instance, I think it’s potentially rather illuminating that “diction” and “elegance” change in closely correlated ways in the late eighteenth and early nineteenth century. It’s interesting that they peak at the same time, and I might even be willing to say that the dip they both display, in the radical decade of the 1790s, suggests that they had a similar kind of social significance. But of course there will be dozens of other terms (and perhaps thousands of phrases) that also correlate with this profile of change, and the Google dataset won’t do anything to tell us whether they actually occurred in the same sorts of books. This could be a case of unrelated genres that happened to have emerged at the same time.

But I think a list of chronologically correlated terms could tell you a lot if you then took it to an archive with metadata, where Schmidt’s technique of tf-idf clustering could be used to break the list apart into subsets of terms that actually did occur in the same groups of works. In effect this would be a kind of topic modeling, but it would be topic modeling combined with a filter that selects for a particular kind of historical “topicality” or timeliness. I think this might tell me a lot, for instance, about the social factors shaping the late-eighteenth-century vogue for characterizing writing based on its “diction” — a vogue that, incidentally, has a loose relationship to data mining itself.

I’m not sure whether other humanists would accept this kind of technique as evidence. Schmidt has some shrewd comments on the difference between data mining and assisted reading, and he’s right that humanists are usually going to prefer the latter. Plus, the same “bias” that makes a technique like this useful dispels any illusion that it is a purely objective or self-generating pattern. It’s clearly a tool used to slice an archive from a particular angle, for particular reasons.

But whether I could use it as evidence or not, a technique like this would be heuristically priceless: it would give me a way of identifying topics that peculiarly characterize a period — or perhaps even, as the dip in the 1790s hints, a particular impulse in that period — and I think it would often turn up patterns that are entirely unexpected. It might generate these patterns by looking for correlations between words, but it would then be fairly easy to turn lists of correlated words into lists of works, and investigate those in more traditionally humanistic ways.

For instance, I had no idea that “diction” would correlate with “elegance” until I stumbled on the connection, but having played around with the terms a bit in MONK, I’m already getting a sense that the terms are related not just through literary criticism (as you might expect), but also through historical discourse and (oddly) discourse about the physiology of sensation. I don’t have a tool yet that can really perform Schmidt’s sort of tf-idf clustering, but just to leave you with a sense of the interesting patterns I’m glimpsing, here’s a word cloud I generated in MONK by contrasting eighteenth-century works that contain “elegance” to the larger reference set of all eighteenth-century works. The cloud is based on Dunning’s log likelihood, and limited to adjectives, frankly, just because they’re easier to interpret at first glance.

ElegantWordCloud — Dark adjectives are overrepresented in a corpus of 18c works that contain "elegance," light ones underrepresented.

There’s a pretty clear contrast here between aesthetic and moral discourse, which is interesting to begin with. But it’s also a bit interesting that the emphasis on aesthetics extends into physiological terms like “sensorial,” “irritative,” and “numb,” and historical terms like “Greek” and “Latin.” Moreover, many of the same terms reoccur if you pursue the same strategy with “diction.”

DictionWordCloud — Dark adjectives are overrepresented in a corpus of 18c works containing "diction," light ones underrepresented.

A lot of words here are predictably literary, but again you see sensory terms like “numb,” and historical ones like “Greek,” “Latin,” and “historical” itself. Once again, moreover, moral discourse is interestingly underrepresented. This is actually just one piece of the larger pattern you might generate if you pursued Schmidt’s clustering strategy — plus, Dunning’s is not the same thing as tf-idf clustering, and the MONK corpus of 1000 eighteenth-century works is smaller than one would wish — but the patterns I’m glimpsing are interesting enough to suggest to me that this general kind of approach could tell me a lot of things I don’t yet know about a period.